题目内容
13.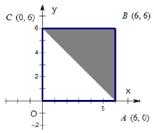 如图:区域A是正方形OABC(含边界),区域B是三角形ABC(含边界).
如图:区域A是正方形OABC(含边界),区域B是三角形ABC(含边界).(Ⅰ)向区域A随机抛掷一粒黄豆,求黄豆落在区域B的概率;
(Ⅱ)若x,y分别表示甲、乙两人各掷一次骰子所得的点数,求点(x,y)落在区域B的概率.
分析 (Ⅰ)根据三角形和正方形的面积之比求出满足条件的概率即可;(Ⅱ)求出落在B内的可能,从而求出满足条件的概率即可.
解答 解:(Ⅰ)向区域A随机抛掷一枚黄豆,
黄豆落在区域B的概率$P=\frac{S_B}{S_A}=\frac{1}{2}$;
(Ⅱ)甲、乙两人各掷一次骰子,
占(x,y)共36种结可能.
其中落在B内的有26种可能,
即(1,5),(1,6),(2,4),(2,5),(2,6),
(3,3),(3,4),(3,5),(3,6),(4,2),
(4,3),(4,4),(4,5),(4,6),(5,1),
(5,2),(5,3),(5,4),(5,5),(5,6),
(6,1),(6,2),(6,3),(6,4),(6,5),(6,6),
点(x,y)落在区B的概率p=$\frac{26}{36}$=$\frac{13}{18}$.
点评 本题考查了几何概型问题,考查列举法求概率问题,是一道基础题.

练习册系列答案
相关题目
3.设集合A=[-1,2],B={y|y=x2,x∈A},则A∩B=( )
| A. | [1,4] | B. | [1,2] | C. | [-1,0] | D. | [0,2] |
4.已知集合A={1,2,3},B={x∈Z|(x+2)(x-3)<0},则A∪B( )
| A. | {1} | B. | {-1,0,1,2,3} | C. | {1,2} | D. | {0,1,2,3} |
8. 某几何体的三视图如图所示,且该几何体的体积是12,则正视图中的x的值是( )
某几何体的三视图如图所示,且该几何体的体积是12,则正视图中的x的值是( )
 某几何体的三视图如图所示,且该几何体的体积是12,则正视图中的x的值是( )
某几何体的三视图如图所示,且该几何体的体积是12,则正视图中的x的值是( )| A. | 3 | B. | 4 | C. | 9 | D. | 6 |
18.若k∈R,则“k>1”是方程“$\frac{x^2}{k-1}+\frac{y^2}{k+1}=1$”表示椭圆的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 即不充分也不必要条件 |
5.已知不等式x2-ax+a-2>0的解集为(-∞,x1)∪(x2+∞),其中x1<0<x2,则${x_1}+{x_2}+\frac{2}{x_1}+\frac{2}{x_2}$的最大值为( )
| A. | $\frac{3}{2}$ | B. | 0 | C. | 2 | D. | $-\frac{3}{2}$ |
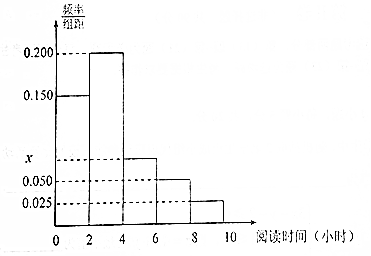 某学校为了了解本校高一学生每周课外阅读时间(单位:小时)的情况,按10%的比例对该校高一600名学生进行抽样统计,将样本数据分为5组:第一组[0,2),第二组[2,4),第三组[4,6),第四组[6,8),第五组[8,10),并将所得数据绘制成如图所示的频率分布直方图:
某学校为了了解本校高一学生每周课外阅读时间(单位:小时)的情况,按10%的比例对该校高一600名学生进行抽样统计,将样本数据分为5组:第一组[0,2),第二组[2,4),第三组[4,6),第四组[6,8),第五组[8,10),并将所得数据绘制成如图所示的频率分布直方图: