题目内容
19.已知等差数列{an}满足:a4>0,a5<0,则满足$\frac{{a}_{n+1}}{{a}_{n}}$>2的n的集合是{5}.分析 根据题意可得d<0,前4项为正数,从5项开始为负数,由$\frac{{a}_{n+1}}{{a}_{n}}$>2得到$\left\{\begin{array}{l}{n-2≤3}\\{n-1≥4}\end{array}\right.$,解得即可
解答 解:已知等差数列{an}满足:a4>0,a5<0,
则d<0,前4项为正数,从5项开始为负数,
由$\frac{{a}_{n+1}}{{a}_{n}}$>2得$\frac{{a}_{n+1}-2{a}_{n}}{{a}_{n}}$>0,
即$\frac{{a}_{1}+nd-2{a}_{1}-2(n-1)d}{{a}_{1}+(n-1)d}$>0,
∴$\frac{{a}_{1}+nd-2d}{{a}_{1}+(n-1)d}$<0,
∴a1+(n-2)d>0,a1+(n-1)d<0,
∴$\left\{\begin{array}{l}{n-2≤3}\\{n-1≥4}\end{array}\right.$,解得n=5,
故答案为:{5}.
点评 本题考查了等差数列的性质和和通项公式,属于中档题

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
10.已知函数f(x)=Asin(ωx+φ),x∈R(其中$A>0,ω>0,0<Φ<\frac{π}{2}$)的图象与x轴的交点中,相邻的两个交点之间的距离为$\frac{π}{2}$,且图象上的一个最低点为$M(\frac{2π}{3},-2)$,则f(x)的解析式为( )
| A. | $f(x)=2sin(2x+\frac{π}{6})$ | B. | $f(x)=2cos(2x+\frac{π}{6})$ | C. | $f(x)=sin(2x+\frac{π}{3})$ | D. | $f(x)=cos(2x+\frac{π}{3})$ |
8.已知a=log23,b=log47,$c={0.3^{-\frac{3}{2}}}$,则a,b,c的大小关系为( )
| A. | b>a>c | B. | a>b>c | C. | c>a>b | D. | c>b>a |
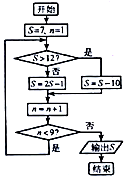 阅读如图的程序框图,运行相应的程序,则输出的S值为3.
阅读如图的程序框图,运行相应的程序,则输出的S值为3.