题目内容
7.等差数列{an}的前n项的和为Sn,且a6与a2012是方程x2-20x+36=0的两根,则$\frac{{S}_{2017}}{2017}$+a1009=( )| A. | 10 | B. | 15 | C. | 20 | D. | 40 |
分析 a6与a2012是方程x2-20x+36=0的两根,a6+a2012=20=2a1009,再利用求和公式与性质即可得出.
解答 解:∵a6与a2012是方程x2-20x+36=0的两根,
∴a6+a2012=20=2a1009,
∴$\frac{{S}_{2017}}{2017}$+a1009=$\frac{2017×\frac{{a}_{1}+{a}_{2017}}{2}}{2017}$+a1009=2a1009=20,
故选:C
点评 本题考查了等差数列的通项公式与求和公式及其性质、一元二次方程的根与系数的关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
18.已知全集U=R,集合A={x|x≥-1},集合B={x|y=lg(x-2)},则A∩(∁UB)=( )
| A. | [-1,2) | B. | [-1,2] | C. | [2,+∞) | D. | [-1,+∞) |
15.已知数列{an+81}是公比为3的等比数列,其中a1=-78,则数列{|an|}的前100项和为( )
| A. | $\frac{{{3^{101}}-16203}}{2}$ | B. | $\frac{{{3^{100}}-15387}}{2}$ | C. | $\frac{{{3^{101}}-15387}}{2}$ | D. | $\frac{{{3^{100}}-16203}}{2}$ |
16.随着生活水平的提高,人们对空气质量的要求越来越高,某机构为了解公众对“车辆限行”的态度,随机抽查50人,并将调查情况进行整理后制成如表:
(1)世界联合国卫生组织规定:[15,45)岁为青年,(45,60)为中年,根据以上统计数据填写以下2×2列联表:
(2)判断能否在犯错误的概率不超过0.05的前提下,认为赞成“车柄限行”与年龄有关?
附:${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({a+d})({a+c})({b+d})}}$,其中n=a+b+c+d
独立检验临界值表:
(3)若从年龄[15,25),[25,35)的被调查中各随机选取1人进行调查,设选中的两人中持不赞成“车辆限行”态度的人员为ξ,求随机变量ξ的分布列和数学期望Eξ.
| 年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,60) |
| 频数 | 10 | 10 | 10 | 10 | 10 |
| 赞成人数 | 3 | 5 | 6 | 7 | 9 |
| 青年人 | 中年人 | 合计 | |
| 不赞成 | 16 | 4 | 20 |
| 赞成 | 14 | 16 | 30 |
| 合计 | 30 | 20 | 50 |
附:${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({a+d})({a+c})({b+d})}}$,其中n=a+b+c+d
独立检验临界值表:
| P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |
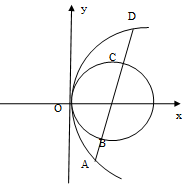 如右图抛物线顶点在原点,圆(x-2)2+y2=22的圆心恰是抛物线的焦点,
如右图抛物线顶点在原点,圆(x-2)2+y2=22的圆心恰是抛物线的焦点,