题目内容
11.已知数列{an}的各项都是正数,a1=1,an+12=an2+$\frac{{a}_{n}}{{n}^{2}}$(n∈N*)(1)求证:$\sqrt{2+\frac{\sqrt{2}(n-2)}{2n}}$≤an<2(n≥2)
(2)求证:12(a2-a1)+22(a3-a2)+…+n2(an+1-an)>$\frac{n}{2}$-$\frac{1}{4}$(n∈N*)
分析 (1)由条件得an2-an-12≥$\frac{\sqrt{2}}{(n-1)^{2}}$,an-12-an-22≥$\frac{\sqrt{2}}{(n-2)^{2}}$,…,a32-a22≥$\frac{\sqrt{2}}{{2}^{2}}$,各式累加后放缩得出结论;
(2)由条件得n2(an+1-an)=$\frac{{a}_{n}}{{a}_{n+1}+{a}_{n}}$=$\frac{1}{2}$-$\frac{{a}_{n+1}-{a}_{n}}{2({a}_{n+1}+{a}_{n})}$>$\frac{1}{2}$-$\frac{1}{4{n}^{2}({a}_{n+1}+{a}_{n})}$$>\frac{1}{2}$-$\frac{1}{8{n}^{2}}$,各式累加后放缩得出结论.
解答 证明:(1)∵an>0,an+12=an2+$\frac{{a}_{n}}{{n}^{2}}$,∴an+1>an,
∴{an}是递增数列.
由a1=1,得a2=$\sqrt{2}$,
当n≥2时,an+12-an2=$\frac{{a}_{n}}{{n}^{2}}$≥$\frac{\sqrt{2}}{{n}^{2}}$,
∴an2-an-12≥$\frac{\sqrt{2}}{(n-1)^{2}}$,an-12-an-22≥$\frac{\sqrt{2}}{(n-2)^{2}}$,…,a32-a22≥$\frac{\sqrt{2}}{{2}^{2}}$,
以上各式相加得:an2-a22≥$\sqrt{2}$($\frac{1}{{2}^{2}}$+$\frac{1}{{3}^{2}}$+…+$\frac{1}{(n-1)^{2}}$),
而$\frac{1}{{2}^{2}}$+$\frac{1}{{3}^{2}}$+…+$\frac{1}{(n-1)^{2}}$≥$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{(n-1)×n}$=($\frac{1}{2}$$-\frac{1}{3}$+$\frac{1}{3}-$$\frac{1}{4}$+…$\frac{1}{n-1}$-$\frac{1}{n}$)=$\frac{n-2}{2n}$,
∴an2-2≥$\frac{\sqrt{2}(n-2)}{2n}$,即an2≥2+$\frac{\sqrt{2}(n-2)}{2n}$,
∴an≥$\sqrt{2+\frac{\sqrt{2}(n-2)}{2n}}$,
又an+12=an2+$\frac{{a}_{n}}{{n}^{2}}$=(an+$\frac{1}{2{n}^{2}}$)2-$\frac{1}{4{n}^{4}}$<(an+$\frac{1}{2{n}^{2}}$)2,
∴an+1<an+$\frac{1}{2{n}^{2}}$,即an+1-an<$\frac{1}{2{n}^{2}}$,
∴an-an-1<$\frac{1}{2(n-1)^{2}}$,an-1-an-2<$\frac{1}{2(n-2)^{2}}$,…,a3-a2<$\frac{1}{2•{2}^{2}}$,a2-a1<$\frac{1}{2•{1}^{2}}$,
以上各式相加得:an-a1<$\frac{1}{2}$($\frac{1}{{1}^{2}}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{(n-1)^{2}}$)<$\frac{1}{2}$(1+$\frac{1}{1×2}$+$\frac{1}{2×3}$+…+$\frac{1}{(n-2)(n-3)}$)=$\frac{1}{2}$(2-$\frac{1}{n-2}$)<1,
∴an<a1+1=2.
(2)∵an+12=an2+$\frac{{a}_{n}}{{n}^{2}}$,
∴n2(an+12-an2)=an,
∴n2(an+1-an)=$\frac{{a}_{n}}{{a}_{n+1}+{a}_{n}}$=$\frac{1}{2}$-$\frac{{a}_{n+1}-{a}_{n}}{2({a}_{n+1}+{a}_{n})}$,
又an+1-an=$\frac{{a}_{n}}{{n}^{2}({a}_{n+1}+{a}_{n})}$<$\frac{1}{2{n}^{2}}$,
∴n2(an+1-an)=$\frac{1}{2}$-$\frac{{a}_{n+1}-{a}_{n}}{2({a}_{n+1}+{a}_{n})}$>$\frac{1}{2}$-$\frac{1}{4{n}^{2}({a}_{n+1}+{a}_{n})}$$>\frac{1}{2}$-$\frac{1}{8{n}^{2}}$,
∴12(a2-a1)+22(a3-a2)+…+n2(an+1-an)>$\frac{n}{2}$-$\frac{1}{8}$($\frac{1}{{1}^{2}}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{3}^{2}}$+…+$\frac{1}{{n}^{2}}$)
>$\frac{n}{2}$-$\frac{1}{8}$(1+$\frac{1}{1×2}$+$\frac{1}{2×3}$+…+$\frac{1}{(n-1)×n}$)=$\frac{n}{2}$-$\frac{1}{8}$(1+1-$\frac{1}{n}$)>$\frac{n}{2}$-$\frac{1}{4}$.
点评 本题考查了不等式的证明,合理使用放缩法是证明的关键,属于中档题.

| A. | C${\;}_{8}^{4}$ | B. | C${\;}_{8}^{2}$ | C. | 24C${\;}_{8}^{4}$ | D. | 22C${\;}_{8}^{2}$ |
| 年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,60) |
| 频数 | 10 | 10 | 10 | 10 | 10 |
| 赞成人数 | 3 | 5 | 6 | 7 | 9 |
| 青年人 | 中年人 | 合计 | |
| 不赞成 | 16 | 4 | 20 |
| 赞成 | 14 | 16 | 30 |
| 合计 | 30 | 20 | 50 |
附:${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({a+d})({a+c})({b+d})}}$,其中n=a+b+c+d
独立检验临界值表:
| P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{5}$ | D. | $\sqrt{6}$ |
| A. | 最小值$\sqrt{2}$ | B. | 最小值2 | C. | 最大值$\sqrt{2}$ | D. | 最大值2 |
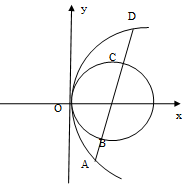 如右图抛物线顶点在原点,圆(x-2)2+y2=22的圆心恰是抛物线的焦点,
如右图抛物线顶点在原点,圆(x-2)2+y2=22的圆心恰是抛物线的焦点,