题目内容
10.在正方体ABCD-A1B1C1D1中,E,F分别是BB1,CD的中点,求证D1F⊥平面ADE.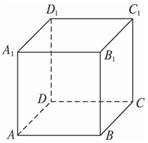
分析 不妨设已知正方体的棱长为1个单位长度,建立空间直角坐标系D-xyz,利用向量数量积为0,证明线线垂直,从而证明线面垂直.
解答 证明:不妨设已知正方体的棱长为1个单位长度,如图所示,建立空间直角坐标系D-xyz,
则$\overrightarrow{AD}=(-1,0,0)$,$\overrightarrow{{D_1}F}=(0,\frac{1}{2},-1)$,$\overrightarrow{AD}•\overrightarrow{{D_1}F}=(-1,0,0)•(0,\frac{1}{2},-1)=0$,∴D1F⊥AD,
又$\overrightarrow{AE}=(0,1,\frac{1}{2})$,$\overrightarrow{AE}•\overrightarrow{{D_1}F}=(0,1,\frac{1}{2})•(0,\frac{1}{2},-1)=0$,
∴D1F⊥AE,AD∩AE=A,所以,D1F⊥平面ADE.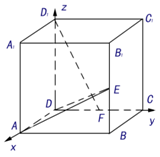
点评 本题考查了空间线面位置关系,考查了向量法证明线面垂直,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.若直线x+y-2=0与直线x-y=0的交点P在角α的终边上,则tanα的值为( )
| A. | 1 | B. | -1 | C. | $\frac{1}{2}$ | D. | $\sqrt{5}$ |
15.已知数列{an+81}是公比为3的等比数列,其中a1=-78,则数列{|an|}的前100项和为( )
| A. | $\frac{{{3^{101}}-16203}}{2}$ | B. | $\frac{{{3^{100}}-15387}}{2}$ | C. | $\frac{{{3^{101}}-15387}}{2}$ | D. | $\frac{{{3^{100}}-16203}}{2}$ |
20.已知x>1,y>1,且log2x,$\frac{1}{4}$,log2y成等比数列,则xy有( )
| A. | 最小值$\sqrt{2}$ | B. | 最小值2 | C. | 最大值$\sqrt{2}$ | D. | 最大值2 |
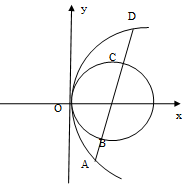 如右图抛物线顶点在原点,圆(x-2)2+y2=22的圆心恰是抛物线的焦点,
如右图抛物线顶点在原点,圆(x-2)2+y2=22的圆心恰是抛物线的焦点,