题目内容
已知椭圆
+y2=1,P是圆x2+y2=16上任意一点,过P作椭圆的切线PA、PB,切点分别为A、B,则
•
的最小值为 .
| x2 |
| 4 |
| PA |
| PB |
考点:椭圆的简单性质
专题:计算题,平面向量及应用,圆锥曲线的定义、性质与方程
分析:设P(m,n),A(x1,y1),B(x2,y2),运用椭圆的一点(x0,y0)处的切线方程:
+y0y=1,求出直线PA,PB的方程,进而得到AB的方程为
+ny=1.代入椭圆方程,利用数量积公式,以及韦达定理,化简整理,结合P是圆x2+y2=16上任意一点,即可求
•
的最小值.
| x0x |
| 4 |
| mx |
| 4 |
| PA |
| PB |
解答:
解:设P(m,n),A(x1,y1),B(x2,y2),
则对
+y2=1两边求导,得,
+2yy′=0,
则过切点A的斜率为-
,切线方程为:y-y1=-
(x-x1),
又x12+4y12=4,化简即得PA:
+y1y=1,
同理可得,PB:
+y2y=1,
∵过P点作椭圆的切线PA,PB,
∴直线AB的方程为
+ny=1.
代入椭圆方程可得(4n2+m2)x2-8mx+(16-16n2)=0,
∴x1+x2=
,x1x2=
,
∴
•
=x1x2+m2-m(x1+x2)+y1y2-n(y1+y2)+n2
=x1x2+m2-m(x1+x2)+
-
+n2
=
+m2+n2-6,
∵m2+n2=16,
∴
•
=11-
,
则当n=0,m=±4时,即P(±4,0),
•
有最小值
.
故答案为:
.
则对
| x2 |
| 4 |
| x |
| 2 |
则过切点A的斜率为-
| x1 |
| 4y1 |
| x1 |
| 4y1 |
又x12+4y12=4,化简即得PA:
| x1x |
| 4 |
同理可得,PB:
| x2x |
| 4 |
∵过P点作椭圆的切线PA,PB,
∴直线AB的方程为
| mx |
| 4 |
代入椭圆方程可得(4n2+m2)x2-8mx+(16-16n2)=0,
∴x1+x2=
| 8m |
| 4n2+m2 |
| 16-16n2 |
| 4n2+m2 |
∴
| PA |
| PB |
=x1x2+m2-m(x1+x2)+
| (4-mx1)(4-mx2) |
| 16n2 |
| 8-m(x1+x2) |
| 4 |
=
| 20-3m2 |
| 4n2+m2 |
∵m2+n2=16,
∴
| PA |
| PB |
| 44 |
| 3n2+16 |
则当n=0,m=±4时,即P(±4,0),
| PA |
| PB |
| 33 |
| 4 |
故答案为:
| 33 |
| 4 |
点评:本题综合考查椭圆的方程及其应用、直线与椭圆的位置关系,考查联立直线方程和椭圆方程,消去未知数,运用韦达定理解题,同时考查了学生的基本运算能力、运算技巧、逻辑推理能力,属于中档题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
设全集M={0,1,2},N={x|x2+x-2≤0},则M∩N=( )
| A、{1} | B、{2} |
| C、{0,1} | D、{1,2} |
关于A到B的一一映射,下列叙述正确的是( )
①一一映射又叫一一对应
②A中的不同元素的像不同
③B中每个元素都有原像
④像的集合就是集合B.
①一一映射又叫一一对应
②A中的不同元素的像不同
③B中每个元素都有原像
④像的集合就是集合B.
| A、①② | B、①②③ |
| C、②③④ | D、①②③④ |
已知G点是△ABC的重心,
⊥
,
+
=
,则λ的值为( )
| AG |
| BG |
| 1 |
| tanA |
| 1 |
| tanB |
| 2λ |
| tanC |
| A、1 | ||
B、
| ||
C、
| ||
D、
|
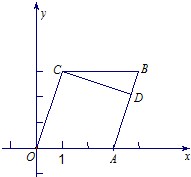 如图,在平行四边形OABC中,点A(3,0),C(1,3),过点C做CD⊥AB于点D.
如图,在平行四边形OABC中,点A(3,0),C(1,3),过点C做CD⊥AB于点D.