题目内容
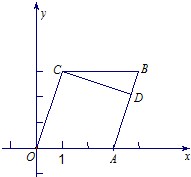 如图,在平行四边形OABC中,点A(3,0),C(1,3),过点C做CD⊥AB于点D.
如图,在平行四边形OABC中,点A(3,0),C(1,3),过点C做CD⊥AB于点D.(1)求CD所在直线的方程;
(2)求D点坐标.
考点:直线的一般式方程与直线的垂直关系,直线的一般式方程
专题:直线与圆
分析:(1)因为直线OC的斜率为3,且CD⊥OC,由此能求出直线CD的斜率为-
,进而能求出直线CD的方程.
(2)因为OC∥AB,所以kOC=kAB,又A(3,0),由此能求出直线AB的方程,联立方程组能求出D点坐标.
| 1 |
| 3 |
(2)因为OC∥AB,所以kOC=kAB,又A(3,0),由此能求出直线AB的方程,联立方程组能求出D点坐标.
解答:
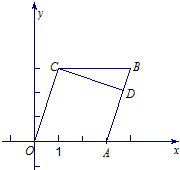 解:(1)因为直线OC的斜率为3且CD⊥OC
解:(1)因为直线OC的斜率为3且CD⊥OC
所以直线CD的斜率为-
…(3分)
所以直线CD的方程为y-3=-
(x-1):
化简得:x+3y-10=0…(6分)
(2)因为OC∥AB,所以kOC=kAB…(8分)
又A(3,0)所以直线AB的方程为:y=3(x-3)…(10分)
联立方程
解得:
所以D(
,
).…(12分)
 解:(1)因为直线OC的斜率为3且CD⊥OC
解:(1)因为直线OC的斜率为3且CD⊥OC所以直线CD的斜率为-
| 1 |
| 3 |
所以直线CD的方程为y-3=-
| 1 |
| 3 |
化简得:x+3y-10=0…(6分)
(2)因为OC∥AB,所以kOC=kAB…(8分)
又A(3,0)所以直线AB的方程为:y=3(x-3)…(10分)
联立方程
|
|
所以D(
| 37 |
| 10 |
| 21 |
| 10 |
点评:本题考查直线方程的求法,考查点的坐标的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
若关于x的不等式cosθ(1-x)2-2x(1-x)+2
x2sinθ≥0对一切x∈[0,1]恒成立,则θ的取值范围是( )
| 2 |
A、[kπ+
| ||||
B、[2kπ+
| ||||
C、[kπ+
| ||||
D、[2kπ+
|
已知空间四边形ABCD,E,F,G,H分别边AB,BC,CD,DA的中点,则EG与FH位置关系是( )
| A、相交 | B、平行 | C、异面 | D、重合 |
如图,PA垂直于正方形ABCD所在平面,则以下关系错误的是( )
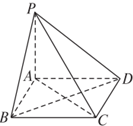

| A、平面PCD⊥平面PAD |
| B、平面PCD⊥平面PBC |
| C、平面PAB⊥平面PBC |
| D、平面PAB⊥平面PAD |
函数f(x)=1-log3x的零点是( )
| A、(1,1) | B、1 |
| C、(3,0) | D、3 |