题目内容
已知函数f(x)=
,若函数y=f(f(x))+1有4个不同的零点,则实数a的取值范围是 .
|
考点:函数零点的判定定理
专题:数形结合,分类讨论,函数的性质及应用
分析:函数y=f[f(x)]+1的零点个数,即为方程f[f(x)]=-1的解的个数,结合函数f(x)图象,分类讨论判断,求解方程可得答案.
解答:
解:函数y=f(f(x))+1的零点,
即方程f[f(x)]=-1的解个数,
(1)当a=0时,f(x)=
,
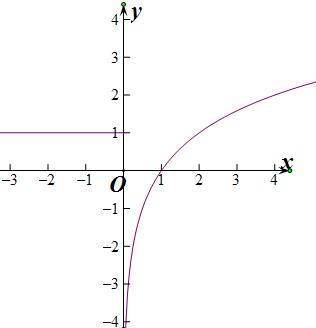
当x>1时,x=
,f(f(x))=-1成立,∴方程f[f(x)]=-1有1解
当0<x<1,log2x<0,∴方程f[f(x)]=-1无解,
当x≤0时,f(x)=1,f(f(x))=0,∴,∴f(f(x))=-1有1解,
故a=0不符合题意,
(2)当a>0时,
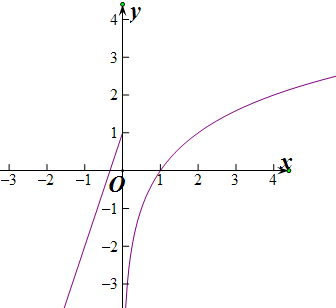
当x>1时,x=
,f(f(x))=-1成立,
当0<x<1,log2x<0,∴方程f[f(x)]=-1有1解,
当
<x≤0时,0<f(x)≤1,∴f(f(x))=-1有1解,
当x≤-
时,f(x)<0,∴f(f(x))=-1有1解,
故,f(f(x))=-1有4解,
(3)当a<0时,
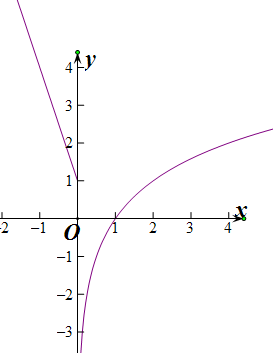
当x>1时,x=
,f(f(x))=-1成立,∴f(f(x))=-1有1解,
当0<x≤1时,f(x)≤0.f(f(x))=-1,成立∴f(f(x))=-1有1解,
当x≤0时,f(x)≥1,f(f(x))=-1,成立∴f(f(x))=-1有1解,
故f(f(x))=-1有3解,
不符合题意,
综上;a>0
故答案为:(0,+∞)
即方程f[f(x)]=-1的解个数,
(1)当a=0时,f(x)=
|
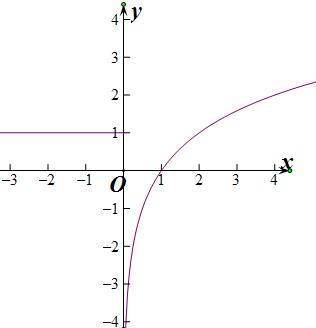
当x>1时,x=
| 2 |
当0<x<1,log2x<0,∴方程f[f(x)]=-1无解,
当x≤0时,f(x)=1,f(f(x))=0,∴,∴f(f(x))=-1有1解,
故a=0不符合题意,
(2)当a>0时,
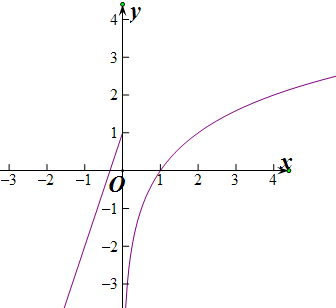
当x>1时,x=
| 2 |
当0<x<1,log2x<0,∴方程f[f(x)]=-1有1解,
当
| 1 |
| a |
当x≤-
| 1 |
| a |
故,f(f(x))=-1有4解,
(3)当a<0时,
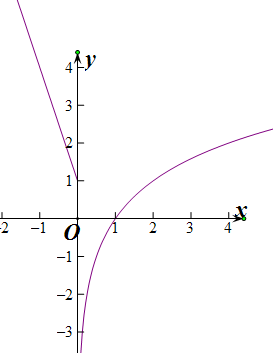
当x>1时,x=
| 2 |
当0<x≤1时,f(x)≤0.f(f(x))=-1,成立∴f(f(x))=-1有1解,
当x≤0时,f(x)≥1,f(f(x))=-1,成立∴f(f(x))=-1有1解,
故f(f(x))=-1有3解,
不符合题意,
综上;a>0
故答案为:(0,+∞)
点评:本题考查的知识点是函数零点的判定,其中将函数的零点问题转化为方程根的个数问题,分类讨论求解.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
设集合M={m∈Z|-3<m<2},N={n∈N|-1≤n≤3},则M∩N=( )
| A、{0,1} |
| B、{-1,0,1} |
| C、{0,1,2} |
| D、{-1,0,1,2} |
已知点M(
,3)在幂函数f(x)的图象上,则f(x)的表达式为( )
| 3 |
A、f(x)=x
| ||
B、f(x)=x-
| ||
| C、f(x)=x2 | ||
| D、f(x)=x-2 |