题目内容
设不等式组
4表示的平面区域为D.
(1)在直角坐标系中画出平面区域D;
(2)若直线y=kx+
分平面区域D为面积相等的两部分,求k的值.
|
(1)在直角坐标系中画出平面区域D;
(2)若直线y=kx+
| 4 |
| 3 |
考点:简单线性规划
专题:不等式的解法及应用
分析:(1)通过约束条件直接在直角坐标系中画出平面区域D;
(2)利用直线y=kx+
恒过的定点,推出在经过的其它点的坐标.即可解决直线分平面区域D为面积相等的两部分,从而求k的值.
(2)利用直线y=kx+
| 4 |
| 3 |
解答:
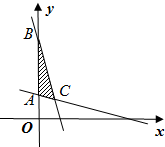 解:(1)如图所示,区域D为△ABC内部及其边界;…(6分)
解:(1)如图所示,区域D为△ABC内部及其边界;…(6分)
(2)依题可知,直线y=kx+
恒过定点A(0,
),…(8分),
B(0,4),由
解得C(1,1)
直线y=kx+
分区域D为面积相等的两部分,
则直线经过线段BC的中点M(
,
),…(10分)
所以k=
=
.…(12分)
 解:(1)如图所示,区域D为△ABC内部及其边界;…(6分)
解:(1)如图所示,区域D为△ABC内部及其边界;…(6分)(2)依题可知,直线y=kx+
| 4 |
| 3 |
| 4 |
| 3 |
B(0,4),由
|
直线y=kx+
| 4 |
| 3 |
则直线经过线段BC的中点M(
| 1 |
| 2 |
| 5 |
| 2 |
所以k=
| ||||
|
| 7 |
| 3 |
点评:本题考查线性规划的应用,恒过定点的直线方程的应用,考查分析问题解决问题的能力.

练习册系列答案
相关题目
已知△ABC满足c=2acosB,则△ABC的形状是( )
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、等腰三角形或直角三角形 |
若关于x的不等式cosθ(1-x)2-2x(1-x)+2
x2sinθ≥0对一切x∈[0,1]恒成立,则θ的取值范围是( )
| 2 |
A、[kπ+
| ||||
B、[2kπ+
| ||||
C、[kπ+
| ||||
D、[2kπ+
|
如图,PA垂直于正方形ABCD所在平面,则以下关系错误的是( )
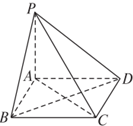

| A、平面PCD⊥平面PAD |
| B、平面PCD⊥平面PBC |
| C、平面PAB⊥平面PBC |
| D、平面PAB⊥平面PAD |