题目内容
给出下列四个命题:
(1)“cosα=-
”是“α=2kπ+
,k∈Z”的必要不充分条件;
(2)终边在y轴上的角的集合是{a|a=
,k∈Z}.
(3)函数y=sin(2x-
)的一个单调增区间是[-
,
];
(4)设f(x)=sin(ωx+φ),其中ω>0,则f(x)是偶函数的充要条件是f′(0)=0;
(5)为得到函数y=cos(2x+
)的图象,只需将函数y=sin2x的图象向左平移
个长度单位.
其中真命题的序号是 (把所有真命题的序号都填上).
(1)“cosα=-
| ||
| 2 |
| 5π |
| 6 |
(2)终边在y轴上的角的集合是{a|a=
| kπ |
| 2 |
(3)函数y=sin(2x-
| π |
| 3 |
| π |
| 12 |
| 5π |
| 12 |
(4)设f(x)=sin(ωx+φ),其中ω>0,则f(x)是偶函数的充要条件是f′(0)=0;
(5)为得到函数y=cos(2x+
| π |
| 3 |
| 5π |
| 12 |
其中真命题的序号是
考点:命题的真假判断与应用
专题:三角函数的图像与性质
分析:(1)解出cosα=-
,再由充分必要条件的定义即可判断;
(2)求出终边在y轴上的角的集合,注意分正半轴和负半轴,再合并,即可判断;
(3)运用正弦函数的单调增区间,求出x的范围,再令k,即可判断;
(4)根据偶函数的定义,化简三角函数式,得到cosφ=0,再求出函数的导数,求出f′(0)=0则cosφ=0,从而加以判断;
(5)根据三角函数的图象平移规律,向左右平移,是针对自变量x而言,必须提取系数,然后运用诱导公式,即可判断.
| ||
| 2 |
(2)求出终边在y轴上的角的集合,注意分正半轴和负半轴,再合并,即可判断;
(3)运用正弦函数的单调增区间,求出x的范围,再令k,即可判断;
(4)根据偶函数的定义,化简三角函数式,得到cosφ=0,再求出函数的导数,求出f′(0)=0则cosφ=0,从而加以判断;
(5)根据三角函数的图象平移规律,向左右平移,是针对自变量x而言,必须提取系数,然后运用诱导公式,即可判断.
解答:
解:(1)由cosα=-
得α=2kπ+
或2kπ+
,k∈Z,故“cosα=-
”是“α=2kπ+
,k∈Z”的必要不充分条件,故(1)正确;
(2)终边在y轴上的角的集合为{α|α=2kπ+
或2kπ+
,k∈Z}={α|α=kπ+
,k∈Z},故(2)错;
(3)令2kπ-
≤2x-
≤2kπ+
,则kπ-
≤x≤kπ+
,k∈Z,则函数y=sin(2x-
)的单调增区间是[kπ-
,kπ+
],k∈Z,当k=0时,即为区间[-
,
],故(3)正确;
(4)设f(x)=sin(ωx+φ),其中ω>0,则f(x)是偶函数,有f(-x)=f(x),即sin(-ωx+φ)=sin(ωx+φ),化简得cosφ=0,又f′(x)=ωcos(ωx+φ),若f′(0)=0则cosφ=0,故f(x)是偶函数的充要条件是f′(0)=0,即(4)正确;
(5)将函数y=sin2x的图象向左平移
个长度单位,得到函数y=sin2(x+
)即y=sin(2x+
+
),即y=cos(2x+
),故(5)正确.
故答案为:(1)(3)(4)(5).
| ||
| 2 |
| 5π |
| 6 |
| 7π |
| 6 |
| ||
| 2 |
| 5π |
| 6 |
(2)终边在y轴上的角的集合为{α|α=2kπ+
| π |
| 2 |
| 3π |
| 2 |
| π |
| 2 |
(3)令2kπ-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| π |
| 12 |
| 5π |
| 12 |
| π |
| 3 |
| π |
| 12 |
| 5π |
| 12 |
| π |
| 12 |
| 5π |
| 12 |
(4)设f(x)=sin(ωx+φ),其中ω>0,则f(x)是偶函数,有f(-x)=f(x),即sin(-ωx+φ)=sin(ωx+φ),化简得cosφ=0,又f′(x)=ωcos(ωx+φ),若f′(0)=0则cosφ=0,故f(x)是偶函数的充要条件是f′(0)=0,即(4)正确;
(5)将函数y=sin2x的图象向左平移
| 5π |
| 12 |
| 5π |
| 12 |
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
故答案为:(1)(3)(4)(5).
点评:本题以命题的真假判断为载体,主要考查三角函数的图象与性质,记熟三角函数的单调区间,图象变换规律是解决该类题的关键.

练习册系列答案
相关题目
已知an=
,n∈N*,则在数列{an}的前50项中最小项和最大项分别是( )
n-
| ||
n-
|
| A、a1,a50 |
| B、a9,a50 |
| C、a9,a8 |
| D、a8,a9 |
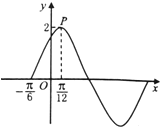 已知函数f(x)=Asin(ωx+φ),(ω>0,A>0,φ∈(0,
已知函数f(x)=Asin(ωx+φ),(ω>0,A>0,φ∈(0, 如图所示,菱形ABCD的边长为
如图所示,菱形ABCD的边长为