题目内容
已知数列{an}的前n项和为Sn,且Sn=
.
(1)求数列{an}的通项公式;
(2)求数列{nan}的前n项和Tn.
| 1-an |
| 2 |
(1)求数列{an}的通项公式;
(2)求数列{nan}的前n项和Tn.
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)利用an与Sn的关系,即可求数列{an}的通项公式;
(2)利用错位相减法即可求数列{nan}的前n项和Tn.
(2)利用错位相减法即可求数列{nan}的前n项和Tn.
解答:
解:(1)∵Sn=
,
∴当n≥2时,an=Sn-Sn-1=
-
,
整理得3an=an-1,即
=
,
当n=1时,a1=
,解得a1=
,
即数列{an}是以a1=
,公比q=
的等比数列,即an=
•(
)n-1=(
)n.
(2)∵nan=n(
)n,
∴{nan}的前n项和Tn=1•
+2•(
)2+…n(
)n,①
Tn=(
)2+2•(
)3+…+(n-1)(
)n+n(
)n+1,②
两式相减得
Tn=
+(
)2+(
)3+…+(
)n-n(
)n+1=
-n(
)n+1=
-
•(
)n-n(
)n+1,
即Tn=
-
•(
)n-
•(
)n+1.
| 1-an |
| 2 |
∴当n≥2时,an=Sn-Sn-1=
| 1-an |
| 2 |
| 1-an-1 |
| 2 |
整理得3an=an-1,即
| an |
| an-1 |
| 1 |
| 3 |
当n=1时,a1=
| 1-a1 |
| 2 |
| 1 |
| 3 |
即数列{an}是以a1=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
(2)∵nan=n(
| 1 |
| 3 |
∴{nan}的前n项和Tn=1•
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
两式相减得
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| ||||
1-
|
| 1 |
| 3 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
即Tn=
| 9 |
| 4 |
| 9 |
| 4 |
| 1 |
| 3 |
| 9n |
| 4 |
| 1 |
| 3 |
点评:本题主要考查数列通项公式的计算,以及利用错位相减法求数列的和,考查学生的计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
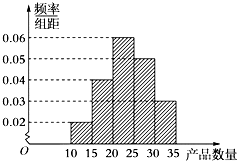 为了调查某厂2000名工人生产某种产品的能力,随机抽查了20位工人某天生产该产品的数量,产品数量的分组区间为[10,15),[15,20),[20,25),[25,30),[30,35],频率分布直方图如图所示.工厂规定从生产低于20件产品的工人中随机地选取2位工人进行培训,则这2位工人不在同一组的概率是( )
为了调查某厂2000名工人生产某种产品的能力,随机抽查了20位工人某天生产该产品的数量,产品数量的分组区间为[10,15),[15,20),[20,25),[25,30),[30,35],频率分布直方图如图所示.工厂规定从生产低于20件产品的工人中随机地选取2位工人进行培训,则这2位工人不在同一组的概率是( )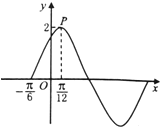 已知函数f(x)=Asin(ωx+φ),(ω>0,A>0,φ∈(0,
已知函数f(x)=Asin(ωx+φ),(ω>0,A>0,φ∈(0,