题目内容
已知椭圆C的焦点在x轴上,且短轴长为4,离心率e=
,
(1)求椭圆C的方程;
(2)若过椭圆C的右焦点F2且斜率为2的直线交椭圆C于A、B两点,求弦AB的长.
| ||
| 5 |
(1)求椭圆C的方程;
(2)若过椭圆C的右焦点F2且斜率为2的直线交椭圆C于A、B两点,求弦AB的长.
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:(1)设出椭圆C的标准方程,由短轴长与离心率,结合a2=b2-c2,求出b、a,即得标准方程;
(2)求出直线AB的方程,与椭圆的方程组成方程组,求出点A、B的坐标,计算出弦长|AB|.
(2)求出直线AB的方程,与椭圆的方程组成方程组,求出点A、B的坐标,计算出弦长|AB|.
解答:
解:(1)根据题意,设椭圆C的方程为
+
=1(a>b>0),
∴2b=4,e=
=
,
又∵a2=b2-c2,
∴b=2,a=
;
∴椭圆C的方程为
+
=1;
(2)∵椭圆C的右焦点为F2(1,0),
∴直线AB的方程为y=2(x-1);
∴
,
解得
,或
;
∴点A(0,-2),B(
,
),
∴弦长|AB|=
=
.
| x2 |
| a2 |
| y2 |
| b2 |
∴2b=4,e=
| c |
| a |
| ||
| 5 |
又∵a2=b2-c2,
∴b=2,a=
| 5 |
∴椭圆C的方程为
| x2 |
| 5 |
| y2 |
| 4 |
(2)∵椭圆C的右焦点为F2(1,0),
∴直线AB的方程为y=2(x-1);
∴
|
解得
|
|
∴点A(0,-2),B(
| 5 |
| 3 |
| 4 |
| 3 |
∴弦长|AB|=
(
|
5
| ||
| 3 |
点评:本题考查了直线与圆锥曲线的应用问题,解题时应熟练地掌握圆锥曲线的几何性质,并能灵活地应用,是基础题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
若平面α的法向量为
1=(3,2,1),平面β的法向量为
=(-2,0,1),则平面α与β夹角(锐角)的余弦是( )
| n |
| n2 |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
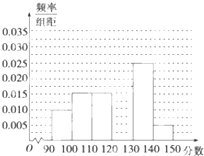 某学校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[90,100),[100,110),…,[140,150)后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
某学校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[90,100),[100,110),…,[140,150)后得到如下部分频率分布直方图.观察图形的信息,回答下列问题: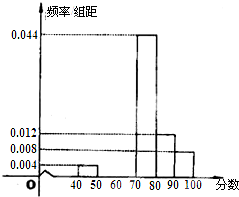 南昌二中某学生社团为了选拔若干名社团义务宣传员,从300名志愿者中随机抽取了50名进行有关知识的测试,成绩(均为整数)按分数段分成六组:第一组[40,50),第二组[50,60),…,第六组[90,100],第一、二、三组的人数依次构成等差数列,如图是按上述分组方法得到的频率分布直方图的一部分.规定成绩不低于66分的志愿者入选为义务宣传员.
南昌二中某学生社团为了选拔若干名社团义务宣传员,从300名志愿者中随机抽取了50名进行有关知识的测试,成绩(均为整数)按分数段分成六组:第一组[40,50),第二组[50,60),…,第六组[90,100],第一、二、三组的人数依次构成等差数列,如图是按上述分组方法得到的频率分布直方图的一部分.规定成绩不低于66分的志愿者入选为义务宣传员. 某种产品特约经销商根据以往当地的需求情况,得出如图该种产品日需求量的频率分布直方图.
某种产品特约经销商根据以往当地的需求情况,得出如图该种产品日需求量的频率分布直方图.