题目内容
10.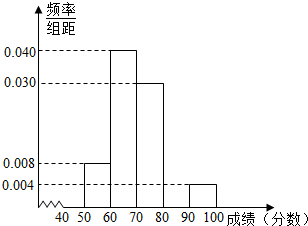 学校从参加高二年级期末考试的学生中抽出一些学生,并统计了他们的数学成绩(成绩均为整数且满分为100分),所得数据整理后,列出了如下频率分布表.
学校从参加高二年级期末考试的学生中抽出一些学生,并统计了他们的数学成绩(成绩均为整数且满分为100分),所得数据整理后,列出了如下频率分布表.(Ⅰ)在给出的样本频率分布表中,求A,B,C的值;
(Ⅱ)补全频率分布直方图,并利用它估计全体高二年级学生期末数学成绩的众数、中位数;
| 分组 | 频数 | 频率 |
| [40,50) | A | 0.04 |
| [50,60) | 4 | 0.08 |
| [60,70) | 20 | 0.40 |
| [70,80) | 15 | 0.30 |
| [80,90) | 7 | B |
| [90,100] | 2 | 0.04 |
| 合计 | C | 1 |
分析 (Ⅰ)利用频率分布表,结合频率,直接求A,B,C的值;
(Ⅱ)求出众数,中位数,画出频率分布直方图即可.
(Ⅲ)利用古典概型概率的求法,求解概率即可.
解答 (本小题满分12分)
解:(Ⅰ)$C=\frac{4}{0.08}=50,A=50×0.04=2,B=\frac{7}{50}=0.14$
(Ⅱ) 众数为最高的小矩形区间中点65,
中位数为$60+\frac{0.4-0.02}{0.4}×10=69.5$;
(Ⅲ)设Ω={从分数在[80,100]的10名同学中随机抽取两名同学},
$n(Ω)=C_9^2=36$.
A={两名学生分数均不低于9(0分)},
n(A)=1,根据古典概型计算公式,$P(A)=\frac{n(A)}{n(Ω)}=\frac{1}{36}$.
点评 本题考查频率分布直方图以及频率分布表的应用,考查计算能力.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
18.已知角θ的始边与x轴的非负半轴重合,终边在直线y=$\frac{1}{2}$x上,则cos2θ=( )
| A. | $-\frac{4}{5}$ | B. | $\frac{4}{5}$ | C. | $-\frac{3}{5}$ | D. | $\frac{3}{5}$ |
5.执行如图所示的程序框图,若输入n的值为7,则输出s的值是( )


| A. | 3 | B. | 15 | C. | 75 | D. | 105 |
19.已知A(3,1),B(-1,2),则直线AB的斜率为( )
| A. | $\frac{1}{7}$ | B. | 0 | C. | $-\frac{1}{4}$ | D. | -3 |
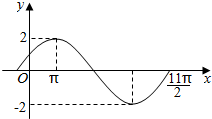 已知函数$f(x)=Asin(ωx+\frac{π}{6})(A>0,ω>0)$)图象的一部分如图所示.
已知函数$f(x)=Asin(ωx+\frac{π}{6})(A>0,ω>0)$)图象的一部分如图所示.