题目内容
5．执行如图所示的程序框图，若输入n的值为7，则输出s的值是（ ）
| A． | 3 | B． | 15 | C． | 75 | D． | 105 |
分析 由已知中的程序框图及已知中输入3，可得：进入循环的条件为i≤3，即i=1，2，3．模拟程序的运行结果，即可得到输出的S值．
解答 解：当i=1时，S=1×1；
当i=2时，S=1×3=3；
当i=3时，S=3×5=15；
当i=4时，退出循环，输出S=15；
故选B．
点评 本题主要考查的知识点是程序框图，在写程序的运行结果时，我们常使用模拟循环的方法，同时考查了运算求解能力，属于基础题
练习册系列答案
名校课堂系列答案
相关题目
13．已知Sn是数列{an}的前n项和，若Sn=1-an，则数列{an}是（ ）
| A． | 等差数列 | B． | 递减的等比数列 | C． | 递增的等比数列 | D． | 不是等比数列 |
13．已知f（x）是周期为3的奇函数，且f（1）=2，则f（8）=（ ）
| A． | 2 | B． | -2 | C． | -1 | D． | 1 |
20．若m是函数f（x）=$\sqrt{x}$-2x+2的一个零点，且x1∈（0，m），x2∈（m，+∞），则f（x1），f（x2），f（m）的大小关系为（ ）
| A． | f（x1）＜f（m）＜f（x2） | B． | f（m）＜f（x2）＜f（x1） | C． | f（m）＜f（x1）＜f（x2） | D． | f（x2）＜f（m）＜f（x1） |
10．
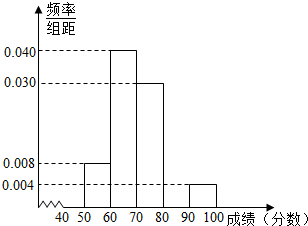学校从参加高二年级期末考试的学生中抽出一些学生，并统计了他们的数学成绩（成绩均为整数且满分为100分），所得数据整理后，列出了如下频率分布表．
（Ⅰ）在给出的样本频率分布表中，求A，B，C的值；
（Ⅱ）补全频率分布直方图，并利用它估计全体高二年级学生期末数学成绩的众数、中位数；
（Ⅲ）现从分数在[80，90），[90，100]的9名同学中随机抽取两名同学，求被抽取的两名学生分数均不低于90分的概率．
学校从参加高二年级期末考试的学生中抽出一些学生，并统计了他们的数学成绩（成绩均为整数且满分为100分），所得数据整理后，列出了如下频率分布表．（Ⅰ）在给出的样本频率分布表中，求A，B，C的值；
（Ⅱ）补全频率分布直方图，并利用它估计全体高二年级学生期末数学成绩的众数、中位数；
| 分组 | 频数 | 频率 |
| [40，50） | A | 0.04 |
| [50，60） | 4 | 0.08 |
| [60，70） | 20 | 0.40 |
| [70，80） | 15 | 0.30 |
| [80，90） | 7 | B |
| [90，100] | 2 | 0.04 |
| 合计 | C | 1 |
17．已知$y=\sqrt{2016}$，则y′=（ ）
| A． | $\frac{1}{{2\sqrt{2016}}}$ | B． | $-\frac{1}{{2\sqrt{2016}}}$ | C． | $\frac{2016}{{\sqrt{2016}}}$ | D． | 0 |