题目内容
二次函数f(x)=-2x2+ax-b的图象与x轴的交点为(-1,0)和(3,0),则函数f(x)的最大值为 .
考点:二次函数的性质
专题:函数的性质及应用
分析:由二次函数f(x)=-2x2+ax-b的图象与x轴的交点为(-1,0)和(3,0),可得-1,3为方程f(x)=-2x2+ax-b=0的两根,由韦达定理构造关于a,b的方程,解方程可求出a,b的值,进而得到函数的解析式,结合二次函数的性质,可得函数f(x)的最大值.
解答:
解:∵二次函数f(x)=-2x2+ax-b的图象与x轴的交点为(-1,0)和(3,0),
∴-1,3为方程f(x)=-2x2+ax-b=0的两根,
故
,
解得:
,
∴f(x)=-2x2+4x+6其最大值为
=8,
故答案为:8
∴-1,3为方程f(x)=-2x2+ax-b=0的两根,
故
|
解得:
|
∴f(x)=-2x2+4x+6其最大值为
| -2×4×6-42 |
| -2×4 |
故答案为:8
点评:本题考查的知识点是二次函数的性质,其中根据已知分析出-1,3为方程f(x)=-2x2+ax-b=0的两根,是解答的关键.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
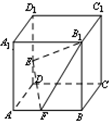 (理科)已知如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别为棱DD1,AB上的点(不含顶点).则下列说法正确的是
(理科)已知如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别为棱DD1,AB上的点(不含顶点).则下列说法正确的是