题目内容
已知
=（λ，2λ），
=（3λ，2），如果
与
的夹角为锐角，则λ的取值范围是 ．
| a |
| b |
| a |
| b |
考点：数量积表示两个向量的夹角
专题：平面向量及应用
分析：由题意可得
•
＞0，去除向量同向的情形即可．
| a |
| b |
解答：
解：∵
与
的夹角为锐角，
∴
•
=3λ2+4λ＞0，
解得λ＜-
或λ＞0，
当2λ=6λ2时两向量共线，
解得λ=0或λ=
，
已知当λ=
时，向量同向，不满足题意，
∴λ的取值范围为：λ＜-
或λ＞0且λ≠
故答案为：λ＜-
或λ＞0且λ≠
| a |
| b |
∴
| a |
| b |
解得λ＜-
| 4 |
| 3 |
当2λ=6λ2时两向量共线，
解得λ=0或λ=
| 1 |
| 3 |
已知当λ=
| 1 |
| 3 |
∴λ的取值范围为：λ＜-
| 4 |
| 3 |
| 1 |
| 3 |
故答案为：λ＜-
| 4 |
| 3 |
| 1 |
| 3 |
点评：本题考查平面向量的数量积与向量的夹角，属基础题．
练习册系列答案
相关题目
方程（
）x+x-3=0的解的个数有（ ）
| 1 |
| 3 |
| A、0个 | B、1个 | C、2个 | D、3个 |
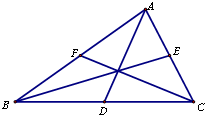如图，△ABC中，D，E，F分别为BC，AC，AB的中点，用坐标法，证明：