题目内容
已知函数f(x)=ax(a>0且a≠1)的图象过点(1,2),设f(x)的反函数为g(x),则不等式g(x)<3的解集为 .
考点:指、对数不等式的解法,反函数
专题:函数的性质及应用
分析:根据条件求出a,利用反函数的关系求解g(x)解不等式即可.
解答:
解:∵函数f(x)=ax(a>0且a≠1)的图象过点(1,2),
∴a=2,即f(x)=2x,
则f(x)的反函数为g(x)=log2x,
由g(x)<3得log2x<3,
解得0<x<8,
故不等式的解集为(0,8),
故答案为:(0,8)
∴a=2,即f(x)=2x,
则f(x)的反函数为g(x)=log2x,
由g(x)<3得log2x<3,
解得0<x<8,
故不等式的解集为(0,8),
故答案为:(0,8)
点评:本题主要考查不等式的求解,考查指数函数和对数函数互为反函数的性质.

练习册系列答案
相关题目
若命题A的逆命题为B,命题A的否命题为C,则B是C的( )
| A、逆命题 | B、否命题 |
| C、逆否命题 | D、都不对 |
设a=log5(2π),b=log5
,c=log6
( )
| 39 |
| 39 |
| A、a>b>c |
| B、a>c>b |
| C、b>a>c |
| D、b>c>a |
函数y=tanπx是( )
| A、周期为1的奇函数 |
| B、周期为π的奇函数 |
| C、周期为1的偶函数 |
| D、周期为2π的偶函数 |
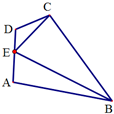 如图,在平面四边形ABCD中,DE=1.EC=
如图,在平面四边形ABCD中,DE=1.EC=