题目内容
已知抛物线的顶点为（-1，-2），且通过（1，10），则这条抛物线的表达式为（ ）
| A、y=3（x-1）2-2 |
| B、y=3（x+1）2+2 |
| C、y=3（x+1）2-2 |
| D、y=-3（x+1）2-2 |
考点：二次函数的性质
专题：函数的性质及应用
分析：根据函数的顶点是（-1，-2），则设抛物线的解析式是：y=a（x+1）2-2，把（1，10）代入函数的解析式即可求得a的值，从而得出函数的解析式．
解答：
解：设抛物线的解析式是：y=a（x+1）2-2，
把（1，10）代入函数的解析式得：4a-2=10，
解得a=3．
则这条抛物线的表达式是：y=3（x+1）2-2．
故选C．
把（1，10）代入函数的解析式得：4a-2=10，
解得a=3．
则这条抛物线的表达式是：y=3（x+1）2-2．
故选C．
点评：本题考查了待定系数法求函数的解析式，根据顶点坐标设出函数的解析式是本题的关键．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
期末集结号系列答案
相关题目
AB是过抛物线x2=y的焦点一条弦，若AB的中点到x轴的距离为1，则弦AB的长度为（ ）
A、
| ||
B、
| ||
| C、2 | ||
| D、3 |
某程序的框图如图所示．执行该程序，若输入的p为16，则输出的n的值为（ ）
| A、3 | B、4 | C、5 | D、6 |
若某程序框图如图所示，则该程序运行后输出的值是（ ）
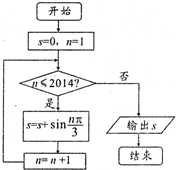
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
抛物线y=x2-2mx+m+2的顶点在第三象限，试确定m的取值范围是（ ）
| A、m＜-1或m＞2 |
| B、m＜0或m＞-1 |
| C、-1＜m＜0 |
| D、m＜-1 |
下列说法中正确的是（ ）
| A、已知a、b为异面直线，过空间中不在a、b上的任意一点，可以作一个平面与a、b都平行 | ||
| B、在二面角α-l-β的两个半平面α、β内分别有直线a、b，则二面角α-l-β是直二面角的充要条件是α⊥β或b⊥a | ||
C、已知异面直线a与b成60°，分别在a、b上的线段AB与CD的长分别为4和2，AC、BD 的中点分别为E、F，则EF=
| ||
D、正三棱锥的内切球的半径为1，则此正三棱锥的体积最小值8
|