题目内容
在△ABC中,角A,B,C所对的边分别为a,b,c,满足
=
.
(1)求角C;
(2)求sinA+sinB的取值范围.
| a+c |
| b |
| sinA-sinB |
| sinA-sinC |
(1)求角C;
(2)求sinA+sinB的取值范围.
考点:正弦定理,余弦定理
专题:三角函数的求值
分析:(1)已知等式右边利用正弦定理化简,整理得到一个关系式,利用余弦定理表示出cosC,将得出的关系式代入求出cosC的值,即可确定出C的度数;
(2)根据C的度数求出A+B的度数,用A表示出B,代入sinA+sinB中,利用两角和与差的正弦函数公式化简,根据A的范围得到这个角的范围,利用正弦函数的值域即可确定出所求式子的范围.
(2)根据C的度数求出A+B的度数,用A表示出B,代入sinA+sinB中,利用两角和与差的正弦函数公式化简,根据A的范围得到这个角的范围,利用正弦函数的值域即可确定出所求式子的范围.
解答:
解:(1)已知等式利用正弦定理化简得:
=
=
,化简得a2+b2-ab=c2,即a2+b2-c2=ab,
∴cosC=
=
,
∵C为三角形的内角,
∴C=
;
(2)∵C=
,∴A+B=π-C=
,即B=
-A,
则sinA+sinB=sinA+sin(
-A)=sinA+
cosA+
sinA=
sinA+
cosA=
sin(A+
),
∵A∈(0,
),∴A+
∈(
,
),
∴sin(A+
)∈(
,1],
则sinA+sinB的取值范围是(
,
].
| a+c |
| b |
| sinA-sinB |
| sinA-sinC |
| a-b |
| a-c |
∴cosC=
| a2+b2-c2 |
| 2ab |
| 1 |
| 2 |
∵C为三角形的内角,
∴C=
| π |
| 3 |
(2)∵C=
| π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
则sinA+sinB=sinA+sin(
| 2π |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| ||
| 2 |
| 3 |
| π |
| 6 |
∵A∈(0,
| 2π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
∴sin(A+
| π |
| 6 |
| 1 |
| 2 |
则sinA+sinB的取值范围是(
| ||
| 2 |
| 3 |
点评:此题考查了正弦、余弦定理,两角和与差的正弦函数公式,以及正弦函数的定义域与值域,熟练掌握公式及定理是解本题的关键.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
已知抛物线的顶点为(-1,-2),且通过(1,10),则这条抛物线的表达式为( )
| A、y=3(x-1)2-2 |
| B、y=3(x+1)2+2 |
| C、y=3(x+1)2-2 |
| D、y=-3(x+1)2-2 |
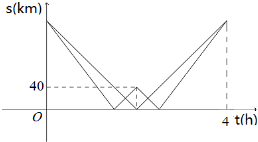 A,B两架直升机同时从机场出发,完成某项救灾物资空投任务.A机到达甲地完成任务后原路返回;B机路过甲地,前往乙地完成任务后原路返回.如图中折线分别表示A,B两架直升机离甲地的距离s与时间t之间的函数关系.假设执行任务过程中A,B均匀速直线飞行,则B机每小时比A机多飞行
A,B两架直升机同时从机场出发,完成某项救灾物资空投任务.A机到达甲地完成任务后原路返回;B机路过甲地,前往乙地完成任务后原路返回.如图中折线分别表示A,B两架直升机离甲地的距离s与时间t之间的函数关系.假设执行任务过程中A,B均匀速直线飞行,则B机每小时比A机多飞行