题目内容
抛物线y=x2-2mx+m+2的顶点在第三象限，试确定m的取值范围是（ ）
| A、m＜-1或m＞2 |
| B、m＜0或m＞-1 |
| C、-1＜m＜0 |
| D、m＜-1 |
考点：二次函数的性质
专题：函数的性质及应用
分析：利用公式法，y=ax2+bx+c的顶点坐标公式表示出其顶点坐标，根据顶点在第三象限，所以顶点的横坐标和纵坐标都小于0，列出不等式组．
解答：
解：根据题意，
解不等式（1），得m＜0，
解不等式（2），得m＜-1；
所以不等式组的解集为m＜-1．
故选D．
|
解不等式（1），得m＜0，
解不等式（2），得m＜-1；
所以不等式组的解集为m＜-1．
故选D．
点评：本题考查顶点坐标的公式和点所在象限的取值范围，同时考查了不等式组的解法，难度较大．
练习册系列答案
快乐小博士巩固与提高系列答案
相关题目
二次函数y=-x2-2x+1图象的顶点在（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
在△ABC中，BC=
，AC=3，sinC=2sinA，则tan（A-
）的值为（ ）
| 5 |
| π |
| 4 |
A、
| ||
B、
| ||
C、-
| ||
| D、3 |
已知抛物线的顶点为（-1，-2），且通过（1，10），则这条抛物线的表达式为（ ）
| A、y=3（x-1）2-2 |
| B、y=3（x+1）2+2 |
| C、y=3（x+1）2-2 |
| D、y=-3（x+1）2-2 |
已知某空间几何体的三视图（单位：cm）如图所示，则该几何体的体积是（ ）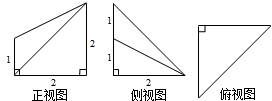
| A、2cm3 | ||
B、
| ||
| C、1cm3 | ||
| D、6cm3 |
已知实数x，y满足不等式组
，则z=x+y的最大值为（ ）
|
| A、15 | B、17 | C、20 | D、30 |