题目内容

6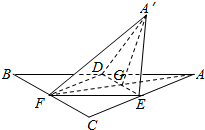．如图，正△ABC的中线AF与中位线DE相交于G，已知△A′ED是△AED绕DE旋转过程中的一个图形，下列命题中，错误的是（　　）
A．动点A′在平面ABC上的射影在线段AF上
B．恒有DE⊥平面A′GF
C．三棱锥A′-FED的体积有最大值
D．异面直线A′E与BD不可能垂直

分析 由△ABC为正三角形可探讨过A'作面ABC的垂线的垂足的位置在AF上，从而可以得到A，B，C正确，通过举反例否定D，即可得答案．

解答 解：过A′作A'H⊥面ABC，垂足为H，
∵△ABC为正三角形且中线AF与中位线DE相交
∴AG⊥DE，A′G⊥DE，
又∵AG∩A′G=G
∴DE⊥面A′GA，
∴H在AF上，故恒有平面A′GF⊥平面BCED，故A，B对．
S三棱锥A′-FED=$\frac{1}{3}$S△EFD•A′H，
∵底面面积是个定值，
∴当A′H为A′G时，三棱锥的面积最大，故C对；
在△A′ED是△AED绕DE旋转的过程中异面直线A′E与BD可能互相垂直，故D不对
故选：D．

点评 本题主要考查了命题的真假判断与应用，考查空间中点，线，面的位置关系，以及线面，面面垂直的判断和性质，同时也考查了异面直线所成角，是个基础题

练习册系列答案
相关题目
16．设函数f（x）为奇函数，且在（-∞，0）上是减函数，若f（-3）=0，则xf（x）＜0的解集为（　　）
A．（-3，0）∪（3，+∞）B．（-∞，-3）∪（0，3）C．（-∞，-3）∪（3，+∞）D．（-3，0）∪（0，3）
17．函数f（x）=sin（2x-$\frac{π}{3}$）（x∈R）的图象为C，以下结论正确的是①②．（写出所有正确结论的编号）
①图象C关于直线x=$\frac{11π}{12}$对称；
②图象C关于点（$\frac{2π}{3}$，0）对称；
③函数f（x）在区间（-$\frac{π}{12}$，$\frac{5π}{2}$）内是增函数；
④由y=sin2x的图象向右平移$\frac{π}{3}$个单位长度可以得到图象C．
14．已知复数z=$\frac{2}{1+i}$，则|z|等于（　　）
A．2B．$\sqrt{2}$C．2 $\sqrt{2}$D．$\frac{{\sqrt{2}}}{2}$
1．奇函数f（x）的定义域为R．若f（x+2）为偶函数，且f（1）=1，则f（5）+f（8）=（　　）
A．-2B．-1C．0D．1
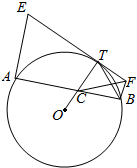11．已知AB是圆O的一条弦，过点A、B分别作AE⊥AB，BF⊥AB，交弧AB上任意一点T的切线于点E、F，OT交AB于点C，求证：
（Ⅰ）∠CBT=∠CFT；
（Ⅱ）CT2=AE•BF．
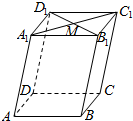18．如图，已知平行六面体ABCD-A1B1C1D1，M为A1C1与B1D1的交点，化简下列向量表达式：
（1）$\overrightarrow{A{A}_{1}}$+$\overrightarrow{{A}_{1}{B}_{1}}$；
（2）$\frac{1}{2}$$\overrightarrow{{A}_{1}{B}_{1}}$+$\frac{1}{2}$$\overrightarrow{A{{\;}_{1}D}_{1}}$；
（3）$\overrightarrow{A{A}_{1}}$+$\frac{1}{2}$$\overrightarrow{{A}_{1}{B}_{1}}$+$\frac{1}{2}$$\overrightarrow{{A}_{1}{D}_{1}}$；
（4）$\overrightarrow{AB}$+$\overrightarrow{BC}$+$\overrightarrow{C{C}_{1}}$+$\overrightarrow{{C}_{1}{A}_{1}}$+$\overrightarrow{{A}_{1}A}$．
15．函数y=2sin（x-$\frac{π}{3}$），x∈[-π，0]的单调增区间为[-$\frac{π}{6}$，0]．
16．函数f（x）=$\frac{{x}^{2}+x-5}{x-2}$，x∈（2，+∞）的最小值为（　　）
A．4B．5C．6D．7

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网