题目内容
15.函数y=2sin(x-$\frac{π}{3}$),x∈[-π,0]的单调增区间为[-$\frac{π}{6}$,0].分析 由条件利用正弦函数的单调性,求得函数的增区间.
解答 解:对于函数函数y=2sin(x-$\frac{π}{3}$),令2kπ-$\frac{π}{2}$≤x-$\frac{π}{3}$≤2kπ+$\frac{π}{2}$,
求得2kπ-$\frac{π}{6}$≤x≤2kπ+$\frac{5π}{6}$,可得函数的增区间为[2kπ-$\frac{π}{6}$,2kπ+$\frac{5π}{6}$],k∈Z.
再结合x∈[-π,0],可得函数的增区间为[-$\frac{π}{6}$,0],
故答案为:[-$\frac{π}{6}$,0].
点评 本题主要考查正弦函数的单调性,属于基础题.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
6.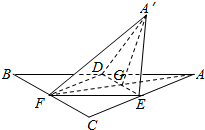 如图,正△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,下列命题中,错误的是( )
如图,正△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,下列命题中,错误的是( )
 如图,正△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,下列命题中,错误的是( )
如图,正△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,下列命题中,错误的是( )| A. | 动点A′在平面ABC上的射影在线段AF上 | |
| B. | 恒有DE⊥平面A′GF | |
| C. | 三棱锥A′-FED的体积有最大值 | |
| D. | 异面直线A′E与BD不可能垂直 |
5.已知函数y=f(x)的定义域为(0,+∞),当x>1时,f(x)<0,且对任意的x,y∈R,恒有f(xy)=f(x)+f(y),则不等式f(x)+f(x-2)≥f(8)的解集为( )
| A. | (2,4] | B. | [-2,4] | C. | [4,+∞) | D. | (-∞,-2]∪[4,+∞) |