题目内容
12.已知圆O的圆心为(2,-1),且圆与直线3x+4y-7=0相切.求:(1)求圆O的标准方程;
(2)圆心O关于直线2x-y+1=0的对称点O′为圆心,半径不变的圆的方程.
分析 (1)利用点到直线的距离公式求出圆心到直线3x+4y-7=0的距离即为圆的半径,根据圆心坐标和求出的半径写出圆的方程即可;
(2)设出(2,-1)关于直线2x-y+1=0的对称点O′为:(a,b),由两点中点在直线上,斜率之积等于-1联立方程组求出所求圆的圆心坐标,即可求出结论.
解答 解:(1)由点(2,-1)到直线3x+4y-7=0的距离d=$\frac{|6-4-7|}{\sqrt{{3}^{2}+{4}^{2}}}=1$,
得圆的半径r=d=1,
则所求的圆的方程为(x-2)2+(y+1)2=1;
(2)设(2,-1)关于直线2x-y+1=0的对称点O′为:(a,b),
则$\left\{\begin{array}{l}{2×\frac{a+2}{2}-\frac{b-1}{2}+1=0}\\{\frac{b+1}{a-2}=-\frac{1}{2}}\end{array}\right.$,
解得a=-$\frac{14}{5}$,b=$\frac{7}{5}$,即O′(-$\frac{14}{5}$,$\frac{7}{5}$),r=1,
则所求的圆的方程为(x+$\frac{14}{5}$)2+(y-$\frac{7}{5}$)2=1.
点评 本题考查圆的标准方程以及圆的切线方程,运用点到直线的距离公式化简求值,是一道基础题.

练习册系列答案
相关题目
1.若函数f(x)为定义在R上的偶函数,其导函数为f′(x),对任意实数x满足xf′(x)>-f(-x),则不等式xf(x)<(1-2x)f(1-2x)的解集是( )
| A. | (0,$\frac{1}{3}$) | B. | ($\frac{1}{3}$,+∞) | C. | (-∞,$\frac{1}{3}$) | D. | (-∞,$\frac{1}{3}$)∪($\frac{1}{3}$,+∞) |
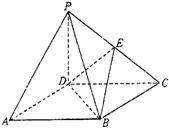 如图,四棱锥P-ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.
如图,四棱锥P-ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.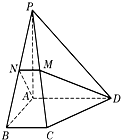 如图,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90°,PA⊥底面ABCD,M、N分别为PC、PB的中点.PA=AB.
如图,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90°,PA⊥底面ABCD,M、N分别为PC、PB的中点.PA=AB.