题目内容
7.用反证法证明2,3,$\sqrt{5}$不可能是一个等差数列中的三项.分析 利用反证法证明,假设2,3,$\sqrt{5}$是同一个等差数列中的三项,分别设为am,an,ap,推出d=$\frac{2-3}{m-n}$为有理数,
又d=$\frac{2-\sqrt{5}}{m-p}$为无理数,矛盾,即可证明不可能是等差数列中的三项.
解答 证明:假设2,3,$\sqrt{5}$是同一个等差数列中的三项,分别设为am,an,ap,
则d=$\frac{2-3}{m-n}$为有理数,
又d=$\frac{2-\sqrt{5}}{m-p}$为无理数,矛盾.
所以,假设不成立,
即2,3,$\sqrt{5}$不可能是同一个等差数列中的三项.
点评 本题考查了反证法的应用问题,也考查了等差数列的应用问题,是基础题目.

练习册系列答案
相关题目
15.下列函数中,在x=0处的导数不等于零的是( )
| A. | y=x3+x2 | B. | y=x+e-x | C. | y=(x-1)e2 | D. | y=xsinx |
19.某校教学大楼共有5层,每层均有2个楼梯,则由一楼至五楼的不同走法共有( )
| A. | 24种 | B. | 52种 | C. | 10种 | D. | 7种 |
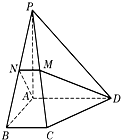 如图,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90°,PA⊥底面ABCD,M、N分别为PC、PB的中点.PA=AB.
如图,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90°,PA⊥底面ABCD,M、N分别为PC、PB的中点.PA=AB.