题目内容
3.已知f(x)是R上的奇函数,f(1)=1,且对任意x∈R都有f(x+6)=f(x)+f(3)成立,则f(2015)+f(2016)=-1.分析 求出f(3)=0,可得f(x)是以6为周期的周期函数,利用函数的周期性和奇偶性进行转化求解,即可得出结论.
解答 解:∵f(x+6)=f(x)+f(3)中,
∴令x=-3,得f(3)=f(-3)+f(3),即f(-3)=0.
又f(x)是R上的奇函数,故f(-3)=-f(3)=0.f(0)=0,
∴f(3)=0,
故f(x+6)=f(x),
∴f(x)是以6为周期的周期函数,
从而f(2015)=f(6×336-1)=f(-1)=-f(1)=-1.
f(2016)=f(6×336)=f(0)=0.
故f(2015)+f(2016)=-1+0=-1,
故答案为:-1
点评 本题主要考查函数值的计算以及奇函数、周期函数的应用,确定f(x)是以6为周期的周期函数是关键.

练习册系列答案
相关题目
13.如图,长方体ABCD-A1B1C1D1中,与直线D1C异面的棱所在的直线有( )条.
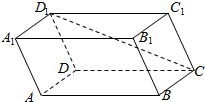

| A. | 2 | B. | 4 | C. | 6 | D. | 7 |
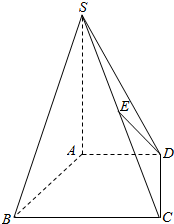 如图,在四棱锥S-ABDC中,底面ABCD是直角梯形,AB垂直于AD和BC,SA⊥底面ABCD,且SA=AB=BC=1,AD=$\frac{1}{2}$,E为SC的中点.
如图,在四棱锥S-ABDC中,底面ABCD是直角梯形,AB垂直于AD和BC,SA⊥底面ABCD,且SA=AB=BC=1,AD=$\frac{1}{2}$,E为SC的中点.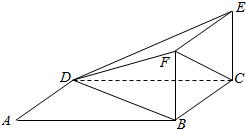 如图.ABCD为平行四边形,BCEF是边长为1的正方形.BF⊥BA,∠DAB=$\frac{π}{3}$,AB=2AD.
如图.ABCD为平行四边形,BCEF是边长为1的正方形.BF⊥BA,∠DAB=$\frac{π}{3}$,AB=2AD.