题目内容
若f（x）=2+log2x，x∈[1，4]，则y=（f（x））2+f（x2）的最大值为 ．
考点：对数函数的图像与性质,对数的运算性质
专题：函数的性质及应用
分析：换元转化y=t2+6t+4，t∈[0，2]根据二次函数性质求解．
解答：
解：∵f（x）=log2x+2，x∈[1，4]，
∴y=[f（x）]2+f（x2）=（log2x+2）2+2log2x=（log2x）2+6log2x+4
设t=log2x则t∈[0，2]
∴y=t2+6t+4=（t+3）2-5，
∴y=t2+6t+4在[0，2]为增函数，
当t=2时，y有最大值，
∴ymax=4+12+4=20
故答案为：20
∴y=[f（x）]2+f（x2）=（log2x+2）2+2log2x=（log2x）2+6log2x+4
设t=log2x则t∈[0，2]
∴y=t2+6t+4=（t+3）2-5，
∴y=t2+6t+4在[0，2]为增函数，
当t=2时，y有最大值，
∴ymax=4+12+4=20
故答案为：20
点评：本题考察了对数函数的性质，二次函数的性质，换元法求解最大值问题，属于中档题．
练习册系列答案
心算口算巧算一课一练系列答案
应用题作业本系列答案
相关题目
已知全集U=R，集合 A={x|-2≤x≤3}，B={x|x＞4或x＜-1}，那么 A∩B=（ ）
| A、{x|-2≤x＜4} |
| B、{x|-2≤x＜-1} |
| C、{x|x≤3或x≥4} |
| D、{x|-1≤x≤3} |
根据表格中的数据，可以判定方程ex-x-6=0的一个根所在的区间为（ ）
| x | -1 | 0 | 1 | 2 | 3 |
| ex | 0.37 | 1 | 2.72 | 7.39 | 20.09 |
| x+6 | 5 | 6 | 7 | 8 | 9 |
| A、（-1，0） |
| B、（0，1） |
| C、（1，2） |
| D、（2，3） |
使函数y=2sin（2x+φ+
）为奇函数，且在[0，
]上是减函数的φ的一个值是（ ）
| π |
| 3 |
| π |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
若某算法框图如图所示，则输出的结果为（ ）
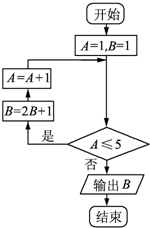
| A、7 | B、15 | C、31 | D、63 |
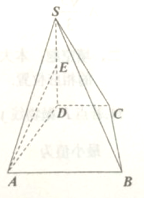如图，在四棱锥S-ABCD中，底面ABCD是直角梯形，AD垂直于AB和CD，侧棱SD⊥底面ABCD，且SD=AD=AB=2CD，点E为棱SD的中点．求异面直线AE和SB所成角的余弦值．