题目内容
有F,G,Y,Z四所学校组织高三教师经验交流,各校参加教师人数具体如下表:(单位:人)
为了进一步搞好高三复习,采用分层抽样的方法从上述四所学校参加经验交流的教师中随机抽取50名教师做经验介绍.
(1)从做经验介绍的50名教师中随机抽取两名,求这两名教师来自同一所学校的概率;
(2)在做经验介绍的50名教师中,从来自G、Y两所学校的教师中随机抽取两名,用X表示抽得G校教师的人数,求X的分布列和数学期望.
| 学校 | F | G | Y | Z |
| 人数 | 60 | 45 | 30 | 15 |
(1)从做经验介绍的50名教师中随机抽取两名,求这两名教师来自同一所学校的概率;
(2)在做经验介绍的50名教师中,从来自G、Y两所学校的教师中随机抽取两名,用X表示抽得G校教师的人数,求X的分布列和数学期望.
考点:离散型随机变量的期望与方差,列举法计算基本事件数及事件发生的概率,离散型随机变量及其分布列
专题:概率与统计
分析:(1)从四所学校中抽取做经验介绍的教师的人数分别为20,15,10,5,从做经验介绍的50名教师中随机抽取两名的取法共有
=1225种,这两名教师来自同一学校的取法共有
+
+
+
=350种,由此能求出这两名教师来自同一所学校的概率.
(2)由已知得X的可能取值为0,1,2,分别求出相应的概率,由此能求出X的分布列和数学期望.
| C | 2 50 |
| C | 2 20 |
| C | 2 15 |
| C | 2 10 |
| C | 2 5 |
(2)由已知得X的可能取值为0,1,2,分别求出相应的概率,由此能求出X的分布列和数学期望.
解答:
解:(1)从四所学校中抽取做经验介绍的教师的人数分别为20,15,10,5…(2分)
从做经验介绍的50名教师中随机抽取两名的取法共有
=1225种,
这两名教师来自同一学校的取法共有
+
+
+
=350种…(5分)
∴这两名教师来自同一所学校的概率P=
=
…(6分)
(2)由(1)知,在做经验介绍的50名教师中,
来自G、Y两校的人数分别为15,10.
X的可能取值为0,1,2,…(7分)
P(X=0)=
=
,
P(X=1)=
=
,
P(X=2)=
=
.
X的分布列为:
EX=0×
+1×
+2×
=
…(12分)
从做经验介绍的50名教师中随机抽取两名的取法共有
| C | 2 50 |
这两名教师来自同一学校的取法共有
| C | 2 20 |
| C | 2 15 |
| C | 2 10 |
| C | 2 5 |
∴这两名教师来自同一所学校的概率P=
| 350 |
| 1225 |
| 2 |
| 7 |
(2)由(1)知,在做经验介绍的50名教师中,
来自G、Y两校的人数分别为15,10.
X的可能取值为0,1,2,…(7分)
P(X=0)=
| ||
|
| 3 |
| 20 |
P(X=1)=
| ||||
|
| 1 |
| 2 |
P(X=2)=
| ||
|
| 7 |
| 20 |
X的分布列为:
| X | 0 | 1 | 2 | ||||||
| P |
|
|
|
| 3 |
| 20 |
| 1 |
| 2 |
| 7 |
| 20 |
| 6 |
| 5 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,在历年高考中都是必考题型之一.

练习册系列答案
相关题目
使函数y=2sin(2x+φ+
)为奇函数,且在[0,
]上是减函数的φ的一个值是( )
| π |
| 3 |
| π |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知f(x)=2sin(2x+
)+1
(1)在直角坐标系中用“五点画图法”画出f(x)一个周期的图象(要求列表、描点)
(2)直接写出函数f(x)的单调递增区间以及f(x)取最大值时的所有x值的集合.
| π |
| 3 |
(1)在直角坐标系中用“五点画图法”画出f(x)一个周期的图象(要求列表、描点)
(2)直接写出函数f(x)的单调递增区间以及f(x)取最大值时的所有x值的集合.
已知命题p:当0<x<2时x2<4,命题q:当b<a<0时b2<a2,则( )
| A、p∧(¬q)为真 |
| B、p∧q为真 |
| C、(¬p)∨q为真 |
| D、(¬p)∧q为真 |
已知点P在圆C:x2+y2=2x+2y上,则点P到直线l:x+y+1=0的距离最大值为( )
A、
| ||||
B、2
| ||||
C、
| ||||
D、3
|
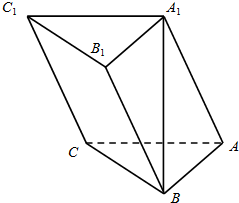 在三棱柱ABC-A1B1C1中,AB⊥AC,A1B⊥平面ABC,且AB=AC=A1B=2.
在三棱柱ABC-A1B1C1中,AB⊥AC,A1B⊥平面ABC,且AB=AC=A1B=2.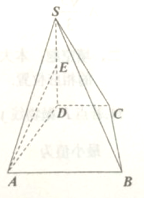 如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,AD垂直于AB和CD,侧棱SD⊥底面ABCD,且SD=AD=AB=2CD,点E为棱SD的中点.求异面直线AE和SB所成角的余弦值.
如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,AD垂直于AB和CD,侧棱SD⊥底面ABCD,且SD=AD=AB=2CD,点E为棱SD的中点.求异面直线AE和SB所成角的余弦值.