Question

13．已知P是△ABC所在平面内一点，D为AB的中点，若2$\overrightarrow{PD}$+$\overrightarrow{PC}$=（λ+1）$\overrightarrow{PA}$+$\overrightarrow{PB}$，且△PBA与△PBC的面积相等，则实数λ的值为-1．

Answer 1

分析 通过D为AB的中点，得到2$\overrightarrow{PD}=\overrightarrow{PA}+\overrightarrow{PB}$，结合已知2$\overrightarrow{PD}$+$\overrightarrow{PC}$=（λ+1）$\overrightarrow{PA}$+$\overrightarrow{PB}$得到$\overrightarrow{PA}+\overrightarrow{PB}$+$\overrightarrow{PC}$=（λ+1）$\overrightarrow{PA}$+$\overrightarrow{PB}$，整理得$\overrightarrow{PC}=λ\overrightarrow{PA}$，利用△PBA与△PBC的面积相等，得到P为AC的中点，求得λ．

解答 解：∵D为AB的中点，
∴2$\overrightarrow{PD}=\overrightarrow{PA}+\overrightarrow{PB}$，
又∵2$\overrightarrow{PD}$+$\overrightarrow{PC}$=（λ+1）$\overrightarrow{PA}$+$\overrightarrow{PB}$，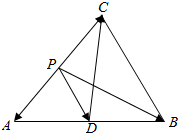
∴$\overrightarrow{PA}+\overrightarrow{PB}$+$\overrightarrow{PC}$=（λ+1）$\overrightarrow{PA}$+$\overrightarrow{PB}$，
∴$\overrightarrow{PC}=λ\overrightarrow{PA}$，
又∵△PBA与△PBC的面积相等，
∴P为AC的中点，所以λ=-1；
故答案为：-1

点评 本题考查平面向量的基本定理以及平面向量的运算，注意解题方法的积累．