题目内容
若f（x）=sinx-cosx，则f′（x）等于（ ）
| A、-cosx-sinx |
| B、cosx-sinx |
| C、sinx+cosx |
| D、-2cosx |
考点：导数的运算
专题：导数的概念及应用
分析：求函数的导数，即可得到结论．
解答：
解：∵f（x）=sinx-cosx，
∴函数的导数为f′（x）=cosx+sinx，
故选：C
∴函数的导数为f′（x）=cosx+sinx，
故选：C
点评：本题主要考查导数的计算，要求熟练掌握常见函数的导数公式．
练习册系列答案
阅读快车系列答案
相关题目
抛物线y2=ax的准线方程是x=-2，则a的值是（ ）
A、
| ||
B、-
| ||
| C、8 | ||
| D、-8 |
已知不共线向量
，
满足|
|=2|
|，且关于x的函数f（x）=-2x3+3|
|x2+6
•
x+5在实数集R上是单调递减函数，则向量
，
的夹角的取值范围是（ ）
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| a |
| b |
A、（0，
| ||
B、（0，
| ||
C、[
| ||
D、[
|
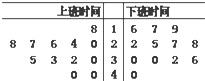
某交警部门对城区上下班交通情况作抽样调查，上下班时间各抽取12辆机动车的行驶速度（单位：km/h）作为样本进行研究，做出样本的茎叶图如图，则上班、下班时间行驶速度的中位数分别是（ ）
| A、28 27.5 |
| B、28 28.5 |
| C、29 27.5 |
| D、29 28.5 |
已知曲线C1：ρ=2和曲线C2：ρcos(θ+
)=
，则C1上到C2的距离等于
的点的个数为（ ）
| π |
| 4 |
| 2 |
| 2 |
| A、0 | B、1 | C、2 | D、3 |
设P为双曲线x2-
=1上的一点，F1，F2是该双曲线的两个焦点，若|PF1|：|PF2|=3：2，则△PF1F2的面积为（ ）
| y2 |
| 12 |
A、6
| ||
| B、12 | ||
C、12
| ||
| D、24 |
曲线y=
x2-2在x=1处的切线的斜率是（ ）
| 1 |
| 2 |
| A、0 | ||
| B、1 | ||
| C、-1 | ||
D、
|