题目内容
已知过点P(m,2)作直线l与圆O:x2+y2=1交于A,B两点,且A为线段PB的中点,则m的取值范围为 .
考点:直线与圆的位置关系
专题:直线与圆
分析:因为A是PB的中点,利用圆x2+y2=1的直径是2,可得PA≤2,即点P到原点距离小于等于3,从而可得结论.
解答:
解:因为A是PB的中点,
∵圆x2+y2=1的直径是2,
∴PA≤2,
∴点P到原点距离小于等于3,
∴m2+4≤9,
∴-
≤m≤
,
∴m的取值范围是[-
,
].
故答案为:[-
,
].
∵圆x2+y2=1的直径是2,
∴PA≤2,
∴点P到原点距离小于等于3,
∴m2+4≤9,
∴-
| 5 |
| 5 |
∴m的取值范围是[-
| 5 |
| 5 |
故答案为:[-
| 5 |
| 5 |
点评:本题考查了直线与圆的位置关系,关键是由已知得到点P到原点距离小于等于3,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
过抛物线y2=10x的焦点作一条直线与抛物线相交于A、B两点,它们的横坐标之和等于5,则这样的直线( )
| A、有且仅有一条 |
| B、有且仅有两条 |
| C、有无穷多条 |
| D、不存在 |
若 a>b,则下列不等式正确的是( )
| A、a2>b2 |
| B、ab>ac |
| C、a-c>b-c |
| D、ac2>bc2 |
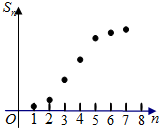 某工厂前n年的总产量Sn与n之间的关系如图所示.从目前记录的结果看,前m年的年平均产量最高.m值为( )
某工厂前n年的总产量Sn与n之间的关系如图所示.从目前记录的结果看,前m年的年平均产量最高.m值为( )| A、2 | B、4 | C、5 | D、8 |
