题目内容

求函数y=-2x+1的单调区间及单调性．
考点：函数单调性的判断与证明
专题：函数的性质及应用
分析：根据一次函数的图象和性质即可得到结论．
解答： 解：根据一次函数的图象和性质知：-2＜0，
则函数y=-2x+1在R上单调递减，即函数的单调递减区间为（-∞，+∞）．
点评：本题主要考查函数单调性和单调区间的求解，根据一次函数的性质是解决本题的关键．
练习册系列答案
相关题目
下列有关命题的说法正确的是（　　）
A、若向量
a
、
b
满足
a
•
b
=0，则
a
=0或者
b
=0
B、“α=30”是“sinα=
1
2
”的必要不充分条件
C、命题“?x∈R，使得x2+x-1＜0”的否定是：“?x∈R，均有x2+x-1＞0”
D、命题“若x=y，则sinx=siny”的逆否命题为真命题
如图，E，F分别在矩形ABCD的边AD，BC上，AB=2，AD=5，AE=1，BF=3，现将四边形AEFB沿EF折起到A′EFB′，使DF⊥B′F．
（Ⅰ）求证：A′E∥平面B′DF
（Ⅱ）求证：平面A′EFB′⊥平面CDEF；
（Ⅲ）求直线B′D与平面A′EFB′所成角的余弦值．
已知
2+
2
3
=2
2
3
，
3+
3
8
=3
3
8
，
4+
4
15
=4
4
15
，…，若
6+
a
t
=6
a
t
（a，t均为正实数）．类比以上等式，可推测a，t的值，则t+a=
 
．
设Sn是数列{an}的前n项和，且2an+Sn=An2+Bn+C．
（1）当A=B=0，C=1时，求an；
（2）若数列{an}为等差数列，且A=1，C=-2．
①求an；
②设bn=2nan，求数列{bn}的前n项和Tn．
已知等差数列{an}，公差d≠0，a1=2，且a1，a3，a9成等比数列．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）求数列{2 an-1}的前n项和Sn．
设圆C与两圆（x+
3
）2+y2=1，（x-
3
）2+y2=1中的一个内切，另一个外切．
（1）求圆心C的轨迹L的方程
（2）求直线y=x+1被轨迹L截得的弦长．
已知方程x2+y2-2（m+3）x+2（1-4m2）y+16m4-7m2+9=0，若该方程表示一个圆，求m的取值范围及圆心的轨迹方程．
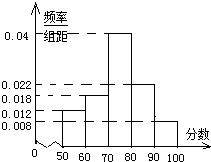某次素质测试，随机抽取了部分学生的成绩，得到如图所示的频率分布直方图．
（1）估计成绩的平均值；
（2）若成绩排名前5的学生中，有一人是学生会主席，从这5人中推荐3人参加自主招生考试，试求这3人中含该学生会主席的概率．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网