题目内容
已知f(x)是偶函数,g(x)是奇函数,且f(x)+g(x)=x2+x+2
(1)求f(x)和g(x)的解析式;
(2)若不等式f(x)≥ag(x)对任意实数x恒成立,求实数a的取值范围.
(1)求f(x)和g(x)的解析式;
(2)若不等式f(x)≥ag(x)对任意实数x恒成立,求实数a的取值范围.
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:(1)根据函数奇偶性的性质利用方程组法即可求f(x)和g(x)的解析式;
(2)根据不等式恒成立进行转化,利用一元二次不等式的性质即可得到结论.
(2)根据不等式恒成立进行转化,利用一元二次不等式的性质即可得到结论.
解答:
解:(1)∵f(x)为偶函数,g(x)为奇函数
∴f(-x)=f(x),g(-x)=-g(x)
又∵f(x)+g(x)=x2+x+2 (1)
∴f(-x)+g(-x)=x2-x+2
∴f(x)-g(x)=x2-x+2 (2)
解(1)(2)联立的方程组得
f(x)=x2+2,g(x)=x.
(2)∵f(x)≥a g(x)对任意实数x恒成立
即x2+2≥ax对任意实数x恒成立
∴x2-ax+2≥0对任意实数x恒成立
∴△=a2-8≤0
∴-2
≤a≤2
.
∴f(-x)=f(x),g(-x)=-g(x)
又∵f(x)+g(x)=x2+x+2 (1)
∴f(-x)+g(-x)=x2-x+2
∴f(x)-g(x)=x2-x+2 (2)
解(1)(2)联立的方程组得
f(x)=x2+2,g(x)=x.
(2)∵f(x)≥a g(x)对任意实数x恒成立
即x2+2≥ax对任意实数x恒成立
∴x2-ax+2≥0对任意实数x恒成立
∴△=a2-8≤0
∴-2
| 2 |
| 2 |
点评:本题主要考查函数的奇偶性的应用以及不等式恒成立问题,根据奇偶性的定义利用方程组法是解决本题的关键.

练习册系列答案
相关题目
已知(x-
)6的展开式中常数项为-160,则常数a=( )
| 2a |
| x |
A、
| ||
B、-
| ||
| C、1 | ||
| D、-1 |
已知函数f(x)=x2+(m2-4)x+m是偶函数,g(x)=xm在(-∞,0)内单调递增,则实数m=( )
| A、2 | B、±2 | C、0 | D、-2 |
下列计算不正确的是( )
| A、log3243=log335=5log33=5×1=5 | ||||
B、log510-log52=log5
| ||||
| C、lg2+lg5=lg(2×5)=lg10=1 | ||||
D、log8(8×4)=log88+log84=1+
|
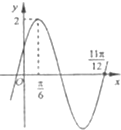 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<