题目内容
已知函数f（x）=
（a≠1）．若f（x）在区间（0，1]上是减函数，则实数a的取值范围是 ．
| ||
| a-1 |
考点：函数单调性的性质
专题：导数的综合应用
分析：求f′（x）=
，根据f（x）在区间（0，1]上是减函数便得到f′（x）＜0，这样可求得a的一个范围，再根据3-ax≥0在（0，1]上恒成立可得到a≤3，所以和前一个a的范围求交集即可得到a的取值范围．
| -a | ||
2(a-1)
|
解答：
解：f′（x）=
；
若f（x）在区间（0，1]上是减函数，则f′（x）＜0；
即
＜0，解得a＜0，或a＞1；
又3-ax≥0，即a≤
，在（0，1]上恒成立，
在（0，1]上的最小值是3，∴a≤3；
∴实数a的取值范围是（-∞，0）∪（1，3]．
故答案为：（-∞，0）∪（1，3]．
| -a | ||
2(a-1)
|
若f（x）在区间（0，1]上是减函数，则f′（x）＜0；
即
| -a |
| a-1 |
又3-ax≥0，即a≤
| 3 |
| x |
| 3 |
| x |
∴实数a的取值范围是（-∞，0）∪（1，3]．
故答案为：（-∞，0）∪（1，3]．
点评：考查函数单调性和函数导数符号的关系，解分式不等式，不要漏了a还需满足3-ax≥0在（0，1]上恒成立．
练习册系列答案
相关题目
已知定义在R上的偶函数f（x）满足f（x-1）=f（x+1），当0≤x≤1时，f（x）=x2，如果函数g（x）=f（x）-（x+m）有两个零点，则实数m的值为（ ）
| A、2k（k∈Z） | ||
B、2k-
| ||
C、2K或2K+
| ||
D、2K或2K-
|
已知函数f（x）=x2+（m2-4）x+m是偶函数，g（x）=xm在（-∞，0）内单调递增，则实数m=（ ）
| A、2 | B、±2 | C、0 | D、-2 |
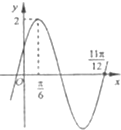已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜