题目内容
一个四面体的三视图如图所示，则该四面体的外接球的表面积为考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：由三视图想象出空间几何体，进而求出几何体外接球的半径，代入球的表面积公式，可得答案．
解答：
解：该几何体是一个正方体截去两个角后所得的组合体，
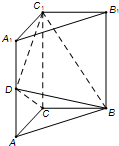
其直观图如图所示：
其外接球即为棱长为1的正方体的外接球，
故其外接球变径R满足：2R=
，
故该四面体的外接球的表面积S=4πR2=3π，
故答案为：3π
其直观图如图所示：
其外接球即为棱长为1的正方体的外接球，
故其外接球变径R满足：2R=
| 3 |
故该四面体的外接球的表面积S=4πR2=3π，
故答案为：3π
点评：本题考查了学生的空间想象力，考查了由三视图得到直观图，其中几何体的形状判断是解答的关键，属于中档题．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
函数y=f（-x）的图象与函数y=f（4+x）的图象关于（ ）
| A、x=4对称 |
| B、x=-4对称 |
| C、x=2对称 |
| D、x=-2对称 |
如图，直三棱柱ABC-A1B1C1中，AC⊥BC，AC=BC=已知定义在R上的偶函数f（x）满足f（x-1）=f（x+1），当0≤x≤1时，f（x）=x2，如果函数g（x）=f（x）-（x+m）有两个零点，则实数m的值为（ ）
| A、2k（k∈Z） | ||
B、2k-
| ||
C、2K或2K+
| ||
D、2K或2K-
|
已知函数f（x）=x2+（m2-4）x+m是偶函数，g（x）=xm在（-∞，0）内单调递增，则实数m=（ ）
| A、2 | B、±2 | C、0 | D、-2 |