题目内容
1.已知α,β是不同的平面,m,n是不同的直线,给出下列命题:①若m?α,n?α,m∥β,n∥β,则α∥β;
②若m?α,n?α,m,n是异面直线,则n与α相交;
③若α∩β=m,n∥m,且n?α,n?β,则n∥α,n∥β.
其中真命题的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 0 |
分析 ①根据面面平行的判定定理,得出①错误;
②根据直线与平面的位置概型得出n与α相交或平行,②错误;
③根据线面平行的判定定理,得出n∥α,n∥β,③正确.
解答 解:对于①,m?α,n?α,m∥β,n∥β,由面面平行的判定定理知,若m∩n=P,则α∥β,∴①错误;
对于②,m?α,n?α,m,n是异面直线,则n与α相交或平行,∴②错误;
对于③,若α∩β=m,n∥m,且n?α,n?β,根据线面平行的判定定理,得出n∥α,n∥β,③正确.
综上,真命题的个数是1.
故选:A.
点评 本题主要考查了线面以及面面之间的位置关系判断问题,也考查了符号语言与空间图形的语言问题,是基础题.

练习册系列答案
 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
12.四个平面互不平行,也不重合,则它们的交线数不可能是( )
| A. | 1条 | B. | 2条 | C. | 4条 | D. | 6条 |
16.函数$f(x)=sin(2x+θ)+\sqrt{3}cos(2x+θ)$为奇函数,且在$[-\frac{π}{4},0]$上为减函数的θ值可以是( )
| A. | $-\frac{π}{3}$ | B. | $-\frac{π}{6}$ | C. | $\frac{5π}{6}$ | D. | $\frac{2π}{3}$ |
6.已知变量x,y满足约束条件$\left\{\begin{array}{l}2x+y≥3\\ y≤x\\ 2x-y≤8\end{array}\right.$,则目标函数z=3x-y的最大值为( )
| A. | 2 | B. | 11 | C. | 16 | D. | 18 |
11.如图,已知圆C的方程为x2+y2=1,P是双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{9}$=1上的一点,过P作圆的两条切线,切点为A,B,则$\overrightarrow{PA}$•$\overrightarrow{PB}$的取值范围为( )
| A. | [0,$\frac{3}{2}$] | B. | [$\frac{3}{2}$,+∞) | C. | [1,$\frac{3}{2}$] | D. | [$\frac{3}{2}$,$\frac{9}{2}$] |
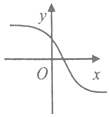
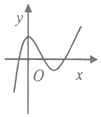
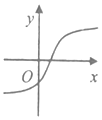
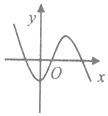
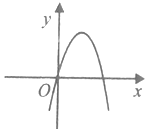 已知函数f(x)的导函数f′(x)=a(x+b)2+c(a≠0)的图象如图所示,则函数f(x)的图象可能是( )
已知函数f(x)的导函数f′(x)=a(x+b)2+c(a≠0)的图象如图所示,则函数f(x)的图象可能是( )