题目内容
16.函数$f(x)=sin(2x+θ)+\sqrt{3}cos(2x+θ)$为奇函数,且在$[-\frac{π}{4},0]$上为减函数的θ值可以是( )| A. | $-\frac{π}{3}$ | B. | $-\frac{π}{6}$ | C. | $\frac{5π}{6}$ | D. | $\frac{2π}{3}$ |
分析 首先根据已知将函数f(x)化简为f(x)=2sin(2x+θ+$\frac{π}{3}$),然后根据函数的奇偶性确定θ的取值,将选项分别代入验证再根据单调性即可排除选项.
解答 解:由已知得:f(x)=2sin(2x+θ+$\frac{π}{3}$),
由于函数为奇函数,故有θ+$\frac{π}{3}$=kπ,
即:θ=kπ-$\frac{π}{3}$(k∈Z),可淘汰B、C选项
然后分别将A和D选项代入检验,
易知当θ=$\frac{2π}{3}$时,
f(x)=-2sin2x其在区间[-$\frac{π}{4}$,0]上递减,
故选D.
点评 本题考查正弦函数的奇偶性和单调性,通过对已知函数的化简,判断奇偶性以及单调性,通过对选项的分析得出结果.考查了对三角函数图象问题的熟练掌握和运用,属于基础题.

练习册系列答案
相关题目
8.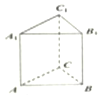 如图,在直三棱柱ABC-A1B1C1中,∠CAB=90°,AC=AB=AA1,则异面直线AC1,A1B所成角的余弦值为( )
如图,在直三棱柱ABC-A1B1C1中,∠CAB=90°,AC=AB=AA1,则异面直线AC1,A1B所成角的余弦值为( )
 如图,在直三棱柱ABC-A1B1C1中,∠CAB=90°,AC=AB=AA1,则异面直线AC1,A1B所成角的余弦值为( )
如图,在直三棱柱ABC-A1B1C1中,∠CAB=90°,AC=AB=AA1,则异面直线AC1,A1B所成角的余弦值为( )| A. | $-\frac{1}{4}$ | B. | $\frac{1}{4}$ | C. | $-\frac{1}{2}$ | D. | $\frac{1}{2}$ |
6.△ABC的内角A,B,C的对边分别为a,b,c,已知cosC=$\frac{1}{4}$,a=1,c=2,则△ABC的面积为( )
| A. | $\frac{\sqrt{15}}{4}$ | B. | $\frac{\sqrt{15}}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |