题目内容
已知直线l：x+my+4=0，若曲线x2+y2+2x-6y+1=0上存在两点P、Q关于直线l对称，则m的值为（ ）
| A、2 | B、-2 | C、1 | D、-1 |
考点：直线与圆的位置关系
专题：直线与圆
分析：曲线x2+y2+2x-6y+1=0上有两点P、Q，满足关于直线x+my+4=0对称，说明曲线是圆，直线过圆心，易求m的值；
解答：
解：曲线方程为（x+1）2+（y-3）2=9表示圆心为（-1，3），半径为3的圆．
∵点P、Q在圆上且关于直线x+my+4=0对称，
∴圆心（-1，3）在直线上．代入得m=-1．
故选：D．
∵点P、Q在圆上且关于直线x+my+4=0对称，
∴圆心（-1，3）在直线上．代入得m=-1．
故选：D．
点评：本题考查直线与圆的方程的应用，圆的一般式方程，考查函数与方程的思想，是中档题．
练习册系列答案
相关题目
数列{an}为等比数列，且an+2=an+1+2an，an＞0，则该数列公比q=（ ）
| A、1 | ||
| B、2 | ||
C、
| ||
D、
|
将4个不同颜色的小球全部放入不同标号的3个盒子中，可以有一个或者多个盒子空着的放法种数为（ ）
| A、96 | B、36 | C、64 | D、81 |
设x，y∈R，向量
=（x，1），
=（1，y），
=（2，-4）且
⊥
，
∥
，则x+y=（ ）
| a |
| b |
| c |
| a |
| c |
| b |
| c |
| A、0 | B、-4 | C、2 | D、4 |
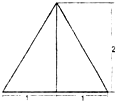一个三棱锥的侧棱长都相等，底面是正三角形，其正（主）视图如右图所示．该三棱锥侧面积和体积分别是（ ）A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、8，
|
tanθ和tan（
-θ）是方程x2+px+q=0的两根，则p与q的关系是（ ）
| π |
| 4 |
| A、p+q+1=0 |
| B、p+q-1=0 |
| C、p-q+1=0 |
| D、p-q-1=0 |
某流程图如图所示，现输入如下四个函数，则可以输出的函数是（ ）
A、f（x）=
| ||||
B、f（x）=ln（
| ||||
C、f（x）=
| ||||
D、f（x）=
|
若P=（x+3）（x+7），Q=（x+4）（x+6），则P，Q的大小关系为（ ）
| A、P＜Q | B、P=Q |
| C、P≤Q | D、P＞Q |