题目内容
3.函数y=-x2+2x+3(x≥0)的值域为( )| A. | [3,+∞) | B. | (-∞,3] | C. | (-∞,4] | D. | [4,+∞) |
分析 求出二次函数的对称轴,利用二次函数的性质求解即可.
解答 解:函数y=-x2+2x+3(x≥0)的开口向下,对称轴为:x=1,可得函数的最大值为:f(1)=4,
∴函数的值域为:(-∞,4].
故选:C.
点评 本题考查二次函数的简单性质的应用,是基础题.

练习册系列答案
相关题目
8.动点A在圆x2+y2=1上移动时,它与定点B(3,0)连线的中点的轨迹方程是( )
| A. | x2+y2+3x+2=0 | B. | x2+y2-3x+2=0 | C. | x2+y2+3y+2=0 | D. | x2+y2-3y+2=0 |
15.某工人生产合格零售的产量逐月增长,前5个月的产量如表所示:请根据所级5组数据,求出y关于x的线性回归方程$\hat y$=x+4.
| 月份x | 1 | 2 | 3 | 4 | 5 |
| 合格零件y(件) | 5 | 6 | 7 | 8 | 9 |
12.命题p:?a∈(-∞,-$\frac{1}{4}$),使得函数f(x)=|x+$\frac{a}{x+1}$|在[$\frac{1}{2}$,3]上单调递增,命题q:g(x)=x+log2x在区间($\frac{1}{2}$,+∞)上无零点,则下列命题中正确的是( )
| A. | ¬p | B. | p∧q | C. | (¬p)∨q | D. | p∧(¬q) |
13.在△ABC中,已知a=$\sqrt{2}$,B=60°,A=45°,则b等于( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{6}$ |
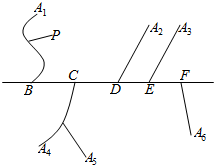 如图,一条公路的两侧有六个村庄,要建一个车站,要求到六个村庄的路程之和最小,应该选在哪里最合适?如果在P的地方增加一个村庄,并且沿地图的虚线修了一条小路,那么这时车站设在什么地方好?
如图,一条公路的两侧有六个村庄,要建一个车站,要求到六个村庄的路程之和最小,应该选在哪里最合适?如果在P的地方增加一个村庄,并且沿地图的虚线修了一条小路,那么这时车站设在什么地方好?