题目内容
已知集合A={x|-2≤x≤1}，B={y|y=2x+3，x∈A}，C={y|y=x2，x∈A}，求B∩C=（ ）
| A、[0，4] |
| B、[-1，5] |
| C、[1，4] |
| D、[-1，4] |
考点：交集及其运算
专题：集合
分析：求解函数的值域化简结合B，C，然后直接利用交集运算得答案．
解答：
解：∵A={x|-2≤x≤1}，
∴B={y|y=2x+3，x∈A}=[-1，5]，
C={y|y=x2，x∈A}=[0，4]，
则B∩C=[0，4]．
故选：A．
∴B={y|y=2x+3，x∈A}=[-1，5]，
C={y|y=x2，x∈A}=[0，4]，
则B∩C=[0，4]．
故选：A．
点评：本题考查了交集及其运算，考查了函数值域的求法，是基础题．
练习册系列答案
相关题目
已知过点A（2，m）和B（m，5）的直线与直线2x-y+1=0平行，则m的值为（ ）
| A、0 | B、1 | C、2 | D、3 |
将87化成二进制数为（ ）
| A、1010111（2） |
| B、1010110（2） |
| C、1110101（2） |
| D、1010101（2） |
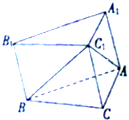如图，在斜三棱柱ABC-A1B1C1的底面△ABC中，∠BAC=90°，且BC1⊥AC，过C1作C1H⊥底面ABC，垂足为H，则点H在（ ）| A、直线AC上 |
| B、直线AB上 |
| C、直线BC上 |
| D、△ABC内部 |
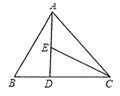如图所示，在△ABC中，