题目内容
已知半圆x2+y2=3（y≥0），P为半圆上任一点，A（2，0）为定点，以PA为边作正三角形PAB，（如图所示）求四边形POAB面积的最大值．考点：同角三角函数基本关系的运用
专题：解三角形
分析：设∠POA=α，由余弦定理表示出PA，即为PB，利用等边三角形的面积公式表示出三角形PAB的面积，进而表示出四边形面积，利用正弦函数的值域确定出最大值即可．
解答：
解：设∠POA=α，由余弦定理得：PA2=4+3-2×2×
cosα=7-4
cosα，
∵PB=PA，
∴S△PAB=
PB2=
（7-4
cosα）=
-3cosα，
∴S四边形=S△PAO+S△PAB=
×2×
sinα+
-3cosα=
sinα-3cosα+
=2
sin（α-
）+
，
当α-
=
，即α=
时，S四边形的最大值为2
+
=
．
| 3 |
| 3 |
∵PB=PA，
∴S△PAB=
| ||
| 4 |
| ||
| 4 |
| 3 |
7
| ||
| 4 |
∴S四边形=S△PAO+S△PAB=
| 1 |
| 2 |
| 3 |
7
| ||
| 4 |
| 3 |
7
| ||
| 4 |
| 3 |
| π |
| 3 |
7
| ||
| 4 |
当α-
| π |
| 3 |
| π |
| 2 |
| 5π |
| 6 |
| 3 |
7
| ||
| 4 |
15
| ||
| 4 |
点评：此题考查了余弦定理，三角形面积公式，以及正弦函数的性质，熟练掌握定理及公式是解本题的关键．
练习册系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
相关题目
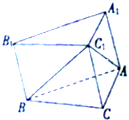如图，在斜三棱柱ABC-A1B1C1的底面△ABC中，∠BAC=90°，且BC1⊥AC，过C1作C1H⊥底面ABC，垂足为H，则点H在（ ）| A、直线AC上 |
| B、直线AB上 |
| C、直线BC上 |
| D、△ABC内部 |
设点（x0，0）在函数f（x）=sin（x-
）-1的图象上，其中
＜x0＜
，则cos（x0-
）的值为（ ）
| π |
| 3 |
| π |
| 2 |
| 4π |
| 3 |
| π |
| 6 |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
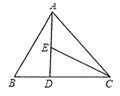如图所示，在△ABC中，