题目内容
已知sin(α+70°)=
,且α是第四象限角,则cos(40°-2α)+sin(α+25°)= .
| 3 |
| 5 |
考点:两角和与差的正弦函数,两角和与差的余弦函数
专题:三角函数的求值
分析:根据三角函数的诱导公式以及倍角公式即可得到结论.
解答:
解:∵α是第四象限角,
∴α+70°是第一象限或者是第四象限角,
∵sin(α+70°)=
,
∴cos(α+70°)=
,
则cos(40°-2α)+sin(α+25°)=cos2(20°-α)+sin[(α+70°)-45°]=
2cos2(20°-α)-1+
[sin(α+70°-cos(α+70°)]
=2sin2(70°+α)-1+
[sin(α+70°-cos(α+70°)]
=2×
+
×(
-
)=
-
,
故答案为:
-
∴α+70°是第一象限或者是第四象限角,
∵sin(α+70°)=
| 3 |
| 5 |
∴cos(α+70°)=
| 4 |
| 5 |
则cos(40°-2α)+sin(α+25°)=cos2(20°-α)+sin[(α+70°)-45°]=
2cos2(20°-α)-1+
| ||
| 2 |
=2sin2(70°+α)-1+
| ||
| 2 |
=2×
| 9 |
| 25 |
| ||
| 2 |
| 3 |
| 5 |
| 4 |
| 5 |
| 18 |
| 25 |
| ||
| 10 |
故答案为:
| 18 |
| 25 |
| ||
| 10 |
点评:本题主要考查三角函数值的计算,根据三角函数的诱导公式以及三角函数的倍角公式是解决本题的关键.综合性较强,运算难度较大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
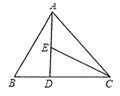 如图所示,在△ABC中,
如图所示,在△ABC中,