题目内容
已知f(α)=
,则f(-
)的值为 .
| sin(180°-α)sin(270°-α)tan(180°-α) |
| sin(90°+α)tan(180°+α)tan(360°-α) |
| 31π |
| 6 |
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:f(α)利用诱导公式化简得到最简结果,将α=-
代入计算即可求出f(-
)的值.
| 31π |
| 6 |
| 31π |
| 6 |
解答:
解:由题意得:f(α)=
=-cosα,
则f(-
)=-cos(-
)=-cos(5π+
)=-cos(π+
)=cos
=
.
故答案为:
| sinα(-cosα)(-tanα) |
| cosαtanα(-tanα) |
则f(-
| 31π |
| 6 |
| 31π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:此题考查了运用诱导公式化简求值,熟练掌握诱导公式是解本题的关键.

练习册系列答案
相关题目
已知角α的终边经过点(12,-5),则sinα等于( )
A、
| ||
B、-
| ||
C、
| ||
D、-
|
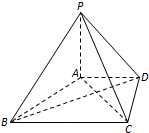 在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,BC=2AD=4,AB=CD=
在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,BC=2AD=4,AB=CD=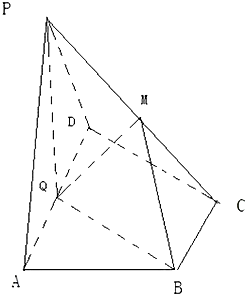 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=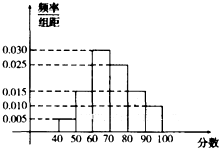 某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分成6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]加以统计,得到如图所示的频率分布直方图.已知高一年级共有学生500名,据此估计,该模块测试成绩不少于60分的学生人数为
某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分成6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]加以统计,得到如图所示的频率分布直方图.已知高一年级共有学生500名,据此估计,该模块测试成绩不少于60分的学生人数为