题目内容

已知向量
a
，
b
，若
a
+
b
与
a
的夹角为
π
3
，
a
+
b
与
b
的夹角为
π
4
，则
|
a
|
|
b
|
=
 
．
考点：平面向量数量积的运算
专题：解三角形
分析：画出图形，结合图形，应用正弦定理，容易解出答案．
解答： 解：如图所示（其中图中字母表示对应向量），
向量
a
+
b
与
a
的夹角为
π
3
，
a
+
b
与
b
的夹角为
π
4
，
∴∠CAB=
π
3
，∠ACB=
π
4
；
由正弦定理，得
AB
sin∠ACB
=
BC
sin∠CAB
，
即
|
a
|
sin
π
4
=
|
b
|
sin
π
3

∴
|
a
|
|
b
|
=
2
2
3
2
=
6
3
；
故答案为：
6
3
．
点评：本题考查了平面向量的基本运算问题，解题时应用数形结合，利用正弦定理解答，就是容易题．
练习册系列答案
相关题目
如图，斜三棱柱ABC-A1B1C1的侧棱长为
2
，底面是边长为1的正三角形，∠A1AB=∠A1AC=45°．
（Ⅰ）求异面直线AA1与BC所成的角；
（Ⅱ）求此棱柱的表面积和体积．
如图，四棱锥P-ABCD中，底面ABCD是边长为2的正方形，PB⊥BC，PD⊥CD，且PA=2，E为PD中点．
（1）求二面角B-EC-A的正弦值；
（2）在线段BC上是否存在点F，使得E到平面PAF的距离为
2
5
5
？若存在，确定点F的位置，若不存在，请说明理由．
已知f（α）=
sin(180°-α)sin(270°-α)tan(180°-α)
sin(90°+α)tan(180°+α)tan(360°-α)
，则f（-
31π
6
）的值为
 
．
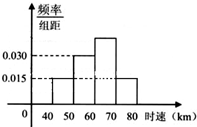已知200辆汽车在通过某一段公路的时速的频率分布直方图如图所示，则时速在[60，70]之间的汽车大约有
 
辆．
已知全集U=R，集合A={x|x＜a}，B═{x|-1＜x＜2}，且A∪∁UB=R，则实数a的取值范围是
 
．
若A（-1，-2），B（4，8），C（5，x），且A、B、C三点共线，则x=
 
．
将长、宽分别为4和3的长方形ABCD沿对角线AC折起，得到四面体A-BCD，则四面体A-BCD的外接球的体积为
 
．
(x+
1
x
)4展开式中的常数项为（　　）
A、6B、8C、10D、12

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网