题目内容
已知x,y均为正实数,且xy=x+y+3,则xy的最小值为 .
考点:基本不等式
专题:创新题型
分析:已知条件提供了和与积的关系,要求的是积的范围,可以考虑将和转化为积,再求积的范围;也可以一元二次方程的韦达定理去研究.
解答:
解:∵x,y均为正实数,且xy=x+y+3
∴xy=x+y+3≥2
+3 (当x=y时取等号)
即 (
)2-2
-3≥0
∴(
+1)(
-3)≥0
∵x,y均为正实数∴
+1>0
∴
-3≥0 即 xy≥9
故xy的最小值为9.
∴xy=x+y+3≥2
| xy |
即 (
| xy |
| xy |
∴(
| xy |
| xy |
∵x,y均为正实数∴
| xy |
∴
| xy |
故xy的最小值为9.
点评:本题主要是用基本不等式解题,关键在于化归转化思想的运用.本题还可以尝试消元利用函数求最值.

练习册系列答案
相关题目
已知复数z满足(1+
i)z=2
i(i为虚数单位),则z在复平面内对应的点位于( )
| 3 |
| 3 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
 如图,在直三棱柱ABC-A1B1C1中,AA1=AB=BC=3,AC=2,D是AC的中点.
如图,在直三棱柱ABC-A1B1C1中,AA1=AB=BC=3,AC=2,D是AC的中点.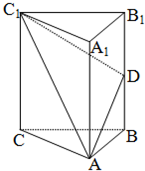 如图,在直三棱柱ABC-A1B1C1中,
如图,在直三棱柱ABC-A1B1C1中, 如图,四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PB⊥BC,PD⊥CD,且PA=2,E为PD中点.
如图,四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PB⊥BC,PD⊥CD,且PA=2,E为PD中点.