题目内容
若cos(α+β)=
,cos(α-β)=
,则tanα•tanβ= .
| 1 |
| 4 |
| 3 |
| 4 |
考点:两角和与差的余弦函数
专题:三角函数的求值
分析:利用两角和与差的余弦函数公式化简已知两等式,再利用同角三角函数间的基本关系化简,即可求出tanα•tanβ的值.
解答:
解:∵cos(α+β)=cosαcosβ-sinαsinβ=
,
cos(α-β)=cosαcosβ+sinαsinβ=
,
∴
=
=
=
,
即3-3tanαtanβ=1+tanαtanβ,
整理得:tanαtanβ=
.
故答案为:
| 1 |
| 4 |
cos(α-β)=cosαcosβ+sinαsinβ=
| 3 |
| 4 |
∴
| cos(α+β) |
| cos(α-β) |
| cosαcosβ-sinαsinβ |
| cosαcosβ+sinαsinβ |
| 1-tanαtanβ |
| 1+tanαtanβ |
| 1 |
| 3 |
即3-3tanαtanβ=1+tanαtanβ,
整理得:tanαtanβ=
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:此题考查了两角和与差的余弦函数公式,以及同角三角函数间的基本关系,熟练掌握公式是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知一个半球的俯视图是一个半径为4的圆,则它的主(正)视图的面积是( )
| A、2π | B、4π | C、8π | D、16π |
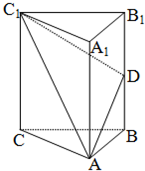 如图,在直三棱柱ABC-A1B1C1中,
如图,在直三棱柱ABC-A1B1C1中,