题目内容
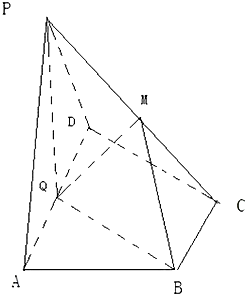 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=| 1 |
| 2 |
| 3 |
(1)求证:平面PQB⊥平面PAD;
(2)若二面角M-QB-C为30°,试确定点M的位置.
考点:用空间向量求平面间的夹角,平面与平面垂直的判定,与二面角有关的立体几何综合题
专题:综合题,空间位置关系与距离,空间角,空间向量及应用
分析:(1)由AD∥BC,BC=
AD,Q为AD的中点,知四边形BCDQ为平行四边形,故CD∥BQ.由∠ADC=90°,知QB⊥AD.由平面PAD⊥平面ABCD,知BQ⊥平面PAD;由此能够证明平面PQB⊥平面PAD;
(2)由PA=PD,Q为AD的中点,知PQ⊥AD.由平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,知PQ⊥平面ABCD.以Q为原点建立空间直角坐标系,利用向量法能够求出t=3.
| 1 |
| 2 |
(2)由PA=PD,Q为AD的中点,知PQ⊥AD.由平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,知PQ⊥平面ABCD.以Q为原点建立空间直角坐标系,利用向量法能够求出t=3.
解答:
(1)证明:∵AD∥BC,BC=
AD,Q为AD的中点,
∴四边形BCDQ为平行四边形,
∴CD∥BQ.
∵∠ADC=90°,∴∠AQB=90,即QB⊥AD.
又∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,
∴BQ⊥平面PAD.
∵BQ?平面PQB,
∴平面PQB⊥平面PAD. …(5分)
(2)解:∵PA=PD,Q为AD的中点,∴PQ⊥AD.
∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,
∴PQ⊥平面ABCD.
如图,以Q为原点建立空间直角坐标系.
则平面BQC的法向量为
=(0,0,1);Q(0,0,0),P(0,0,
),B(0,
,0),C(-1,
,0).
设M(x,y,z),则
=(x,y,z-
),
=(-1-x,
-y,-z),
∵
=t
,…(6分)
∴
,∴
…(9分)
在平面MBQ中,
=(0,
,0),
=(-
,
,
),
∴平面MBQ法向量为
=(
,0,t). …(10分)
∵二面角M-BQ-C为30°,
∴cos30°=
=
=
,
∴t=3,
即M是PC的四等分点. …(12分)
| 1 |
| 2 |
∴四边形BCDQ为平行四边形,
∴CD∥BQ.
∵∠ADC=90°,∴∠AQB=90,即QB⊥AD.
又∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,
∴BQ⊥平面PAD.
∵BQ?平面PQB,
∴平面PQB⊥平面PAD. …(5分)
(2)解:∵PA=PD,Q为AD的中点,∴PQ⊥AD.
∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,
∴PQ⊥平面ABCD.
如图,以Q为原点建立空间直角坐标系.

则平面BQC的法向量为
| n |
| 3 |
| 3 |
| 3 |
设M(x,y,z),则
| PM |
| 3 |
| MC |
| 3 |
∵
| PM |
| MC |
∴
|
|
在平面MBQ中,
| QB |
| 3 |
| QM |
| t |
| 1+t |
| ||
| 1+t |
| ||
| 1+t |
∴平面MBQ法向量为
| m |
| 3 |
∵二面角M-BQ-C为30°,
∴cos30°=
| ||||
|
|
| t | ||
|
| ||
| 2 |
∴t=3,
即M是PC的四等分点. …(12分)
点评:本题考查与二面角有关的立体几何证明题,考查了二面角的求法,面面垂直的证明方法.解题的关键是熟练掌握二面角的平面角的做法以及用向量法求二面角的步骤,面面垂直的相关定理定义等.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
 如图甲,△ABC是边长为6的等边三角形,E,D分别为AB、AC靠近B、C的三等分点,点G为BC边的中点.线段AG交线段ED于F点,将△AED沿ED翻折,使平面AED⊥平面BCDE,连接AB、AC、AG形成如图乙所示的几何体.
如图甲,△ABC是边长为6的等边三角形,E,D分别为AB、AC靠近B、C的三等分点,点G为BC边的中点.线段AG交线段ED于F点,将△AED沿ED翻折,使平面AED⊥平面BCDE,连接AB、AC、AG形成如图乙所示的几何体. 如图,斜三棱柱ABC-A1B1C1的侧棱长为
如图,斜三棱柱ABC-A1B1C1的侧棱长为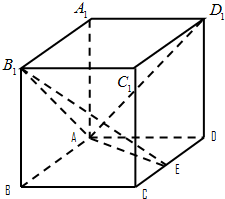 如图,在长方体ABCD-A1B1C1D1中AA1=AD=1,E为CD中点.
如图,在长方体ABCD-A1B1C1D1中AA1=AD=1,E为CD中点.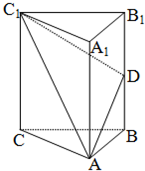 如图,在直三棱柱ABC-A1B1C1中,
如图,在直三棱柱ABC-A1B1C1中, 如图,四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PB⊥BC,PD⊥CD,且PA=2,E为PD中点.
如图,四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PB⊥BC,PD⊥CD,且PA=2,E为PD中点.