题目内容
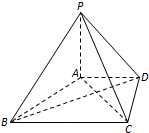 在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,BC=2AD=4,AB=CD=
在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,BC=2AD=4,AB=CD=| 10 |
(Ⅰ)证明:BD⊥平面PAC;
(Ⅱ)若二面角A-PC-D的大小为60°,求AP的值.
考点:与二面角有关的立体几何综合题
专题:综合题,空间位置关系与距离,空间角
分析:(Ⅰ)设O为AC与BD的交点,作DE⊥BC于点E,证明∠BOC=90°,可得AC⊥BD.由PA⊥平面ABCD得PA⊥BD,利用线面垂直的判定定理,可得BD⊥平面PAC;
(Ⅱ)方法一:作OH⊥PC于点H,连接DH,可得∠DHO是二面角A-PC-D的平面角,在Rt△PAC中,
=
,可求AP的值;方法二:以O为原点,OB,OC所在直线为x,y轴,建立空间直角坐标系,求出平面PDC、平面PAC的法向量,利用向量的夹角公式,结合二面角A-PC-D的大小为60°,可求AP的值.
(Ⅱ)方法一:作OH⊥PC于点H,连接DH,可得∠DHO是二面角A-PC-D的平面角,在Rt△PAC中,
| PA |
| PC |
| OH |
| OC |
解答:
 (Ⅰ)证明:设O为AC与BD的交点,作DE⊥BC于点E.
(Ⅰ)证明:设O为AC与BD的交点,作DE⊥BC于点E.
由四边形ABCD是等腰梯形得CE=
=1,DE=
=3,
所以BE=DE,从而得∠DBC=∠BCA=45°,
所以∠BOC=90°,即AC⊥BD.
由PA⊥平面ABCD得PA⊥BD,
因为AC∩PA=A,
所以BD⊥平面PAC. …(7分)
(Ⅱ)解:方法一:作OH⊥PC于点H,连接DH.
由(Ⅰ)知DO⊥平面PAC,故DO⊥PC.
所以PC⊥平面DOH,从而得PC⊥OH,PC⊥DH.
故∠DHO是二面角A-PC-D的平面角,
所以∠DHO=60°.
在Rt△DOH中,由DO=
,得OH=
.
在Rt△PAC中,
=
.
设PA=x,可得
=
.
解得x=
,即AP=
. …(15分)
方法二:(Ⅱ) 由(Ⅰ)知AC⊥BD.以O为原点,OB,OC所在直线为x,y轴,建立空间直角坐标系O-xyz,如图所示.由题意知各点坐标如下: A(0,-
A(0,-
,1),B(2
,0,0),C(0,2
,0),D(-
,0,0).
由PA⊥平面ABCD,得PA∥z轴,
故设点P(0,-
,t) (t>0).
设
=(x,y,z)为平面PDC的法向量,
由
=(-
,-2
,0),
=(-
,
,-t) 知
取y=1,得
=(-2,1,
).
又平面PAC的法向量为
=(1,0,0),于是
|cos<
,
>|=
=
=
.
解得t=
,即AP=
. …(15分)
 (Ⅰ)证明:设O为AC与BD的交点,作DE⊥BC于点E.
(Ⅰ)证明:设O为AC与BD的交点,作DE⊥BC于点E.由四边形ABCD是等腰梯形得CE=
| BC-AD |
| 2 |
| DC2-CE2 |
所以BE=DE,从而得∠DBC=∠BCA=45°,
所以∠BOC=90°,即AC⊥BD.
由PA⊥平面ABCD得PA⊥BD,
因为AC∩PA=A,
所以BD⊥平面PAC. …(7分)
(Ⅱ)解:方法一:作OH⊥PC于点H,连接DH.
由(Ⅰ)知DO⊥平面PAC,故DO⊥PC.
所以PC⊥平面DOH,从而得PC⊥OH,PC⊥DH.
故∠DHO是二面角A-PC-D的平面角,
所以∠DHO=60°.
在Rt△DOH中,由DO=
| 2 |
| ||
| 3 |
在Rt△PAC中,
| PA |
| PC |
| OH |
| OC |
设PA=x,可得
| x | ||
|
| ||
| 6 |
解得x=
3
| ||
| 11 |
3
| ||
| 11 |
方法二:(Ⅱ) 由(Ⅰ)知AC⊥BD.以O为原点,OB,OC所在直线为x,y轴,建立空间直角坐标系O-xyz,如图所示.由题意知各点坐标如下:
 A(0,-
A(0,-| 2 |
| 2 |
| 2 |
| 2 |
由PA⊥平面ABCD,得PA∥z轴,
故设点P(0,-
| 2 |
设
| m |
由
| CD |
| 2 |
| 2 |
| PD |
| 2 |
| 2 |
|
取y=1,得
| m |
3
| ||
| t |
又平面PAC的法向量为
| n |
|cos<
| m |
| n |
|
| ||||
|
|
| 2 | ||||
|
| 1 |
| 2 |
解得t=
3
| ||
| 11 |
3
| ||
| 11 |
点评:本题主要考查空间线、面位置关系,二面角等基础知识,空间向量的应用,同时考查空间想象能力和运算求解能力.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
 如图甲,△ABC是边长为6的等边三角形,E,D分别为AB、AC靠近B、C的三等分点,点G为BC边的中点.线段AG交线段ED于F点,将△AED沿ED翻折,使平面AED⊥平面BCDE,连接AB、AC、AG形成如图乙所示的几何体.
如图甲,△ABC是边长为6的等边三角形,E,D分别为AB、AC靠近B、C的三等分点,点G为BC边的中点.线段AG交线段ED于F点,将△AED沿ED翻折,使平面AED⊥平面BCDE,连接AB、AC、AG形成如图乙所示的几何体. 如图,在直三棱柱ABC-A1B1C1中,AA1=AB=BC=3,AC=2,D是AC的中点.
如图,在直三棱柱ABC-A1B1C1中,AA1=AB=BC=3,AC=2,D是AC的中点. 如图,在四棱锥A-BCDE中,底面四边形BCDE是等腰梯形,BC∥DE,∠DCB=45°,O是BC的中点,AO=
如图,在四棱锥A-BCDE中,底面四边形BCDE是等腰梯形,BC∥DE,∠DCB=45°,O是BC的中点,AO= 如图,斜三棱柱ABC-A1B1C1的侧棱长为
如图,斜三棱柱ABC-A1B1C1的侧棱长为