题目内容
17.过抛物线x2=4y焦点F的直线交抛物线于A,B两点,若|AF|=3,则|BF|的值为( )| A. | 2 | B. | $\frac{1}{2}$ | C. | 1 | D. | $\frac{3}{2}$ |
分析 根据抛物线的定义,结合|AF|=3,求出A的坐标,然后求出AF的方程求出B点的横坐标即可得到结论.
解答 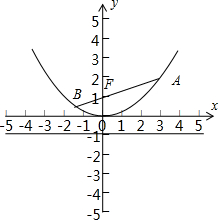 解:抛物线x2=4y,抛物线的焦点F(0,1),
解:抛物线x2=4y,抛物线的焦点F(0,1),
准线方程为y=-1,p=2,
设A(x,y),
则|AF|=y+1=3,故y=2,此时x=2$\sqrt{2}$,即A(2$\sqrt{2}$,2),
kAF=$\frac{2-1}{2\sqrt{2}-0}$=$\frac{\sqrt{2}}{4}$,
则直线AF的方程为:y=$\frac{\sqrt{2}}{4}$x+1,
代入x2=4y,得x2-$\sqrt{2}$x-4=0,
解得x=2$\sqrt{2}$(舍)或x=-$\sqrt{2}$,则y=$\frac{1}{2}$,B(-$\sqrt{2}$,$\frac{1}{2}$)
则|BF|=$\sqrt{(\sqrt{2})^{2}+(1-\frac{1}{2})^{2}}$=$\frac{3}{2}$,
故选:D.
点评 本题主要考查抛物线的弦长的计算,根据抛物线的定义是解决本题的关键.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
8.已知函数f(x)=3sin(2x-$\frac{π}{4}$),则下列结论正确的是( )
| A. | 若f(x1)=f(x2)=0,则x1-x2=kπ(k∈Z) | |
| B. | 函数f(x)的图象关于(-$\frac{π}{8}$,0)对称 | |
| C. | 函数f(x)的图象与g(x)=3cos(2x+$\frac{π}{4}$)的图象相同 | |
| D. | 函数f(x)在[-$\frac{1}{8}$π,$\frac{3}{8}$π]上递增 |
9.已知tan(-α)=3,则$\frac{{{{sin}^2}α-sin2α}}{cos2α}$等于( )
| A. | -$\frac{8}{3}$ | B. | $\frac{8}{3}$ | C. | -$\frac{15}{8}$ | D. | $\frac{15}{8}$ |
6.已知集合I={x∈Z|-3<x<3},A={-2,0,1},B={-1,0,1,2},则(∁IA)∩B等于( )
| A. | {-1} | B. | {2} | C. | {-1,2} | D. | {-1,0,1,2} |
14.某电影公司2012年大陆电影票房为21亿元,若该公司大陆电影票房的年平均增长率为x,2016年大陆电影票房为y亿元,则y与x的函数关系式为( )
| A. | y=84x | B. | y=21(1+4x) | C. | y=21x4 | D. | y=21(1+x)4 |
 如图所示,在三棱柱ABC-A1B1C1中,四边形AA1B1B为边长为2的正方形,四边形BB1C1C为菱形,∠BB1C1=60°,平面AA1B1B⊥平面BB1C1C,点E、F分别是B1C,AA1的中点.
如图所示,在三棱柱ABC-A1B1C1中,四边形AA1B1B为边长为2的正方形,四边形BB1C1C为菱形,∠BB1C1=60°,平面AA1B1B⊥平面BB1C1C,点E、F分别是B1C,AA1的中点.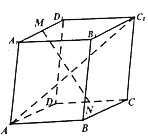 已知平行六面体ABCD-A1B1C1D1,设A1D1中点为M,CD的中点为N,若∠A1AD=∠A1AB=∠BAD=60°且AA1=AB=AD=1,则|AC1|=$\sqrt{6}$,若$\overrightarrow{MN}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$+z$\overrightarrow{A{A}_{1}}$,则x+y+z=0.
已知平行六面体ABCD-A1B1C1D1,设A1D1中点为M,CD的中点为N,若∠A1AD=∠A1AB=∠BAD=60°且AA1=AB=AD=1,则|AC1|=$\sqrt{6}$,若$\overrightarrow{MN}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$+z$\overrightarrow{A{A}_{1}}$,则x+y+z=0.