题目内容
某产品的三个质量指标分别为x,y,z,用综合指标S=x+y+z评价该产品的等级.若S≤4,则该产品为一等品.先从一批该产品中,随机抽取10件产品作为样本,其质量指标列表如下
(1)利用上表提供的样本数据估计该批产品的一等品率;
(2)在该样品中,随机抽取两件产品,设“取出的2件产品的综合指标之差的绝对值”为随机变量ξ
求ξ的分布列和数学期望.
| 产品编号 | A1 | A2 | A3 | A4 | A5 |
| 质量指标(x,y,z) | (1,1,2) | (2,1,1) | (2,2,2) | (1,1,1) | (1,2,1) |
| 产品编号 | A6 | A7 | A8 | A9 | A10 |
| 质量指标(x,y,z) | (1,2,2) | (2,1,1) | (2,2,1) | (1,1,1) | (2,1,2) |
(2)在该样品中,随机抽取两件产品,设“取出的2件产品的综合指标之差的绝对值”为随机变量ξ
求ξ的分布列和数学期望.
考点:离散型随机变量的期望与方差
专题:概率与统计
分析:(1)计算10件产品的综合指票S,得到S≤4的共6件,由此估计该批产品的一等品率为0.6.
(2)ξ的所有可能取值为0、1、2、3,分别求出相应的概率,由此能求出ξ的分布列和数学期望.
(2)ξ的所有可能取值为0、1、2、3,分别求出相应的概率,由此能求出ξ的分布列和数学期望.
解答:
解:(1)计算10件产品的综合指标S,如下表:
其中S≤4的共6件,
∴该样本的一等品率为
=0.6,
由此估计该批产品的一等品率为0.6.(5分)
(2)ξ的所有可能取值为0、1、2、3…6分
P(ξ=0)=
=
,
P(ξ=1)=
=
,
P(ξ=2)=
=
,
P(ξ=3)=
=
…10分
ξ的分布列为:
所以ξ的数学期望为:
.…12分.
| 产品编号 | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 |
| S | 4 | 4 | 6 | 3 | 4 | 5 | 4 | 5 | 3 | 5 |
∴该样本的一等品率为
| 6 |
| 10 |
由此估计该批产品的一等品率为0.6.(5分)
(2)ξ的所有可能取值为0、1、2、3…6分
P(ξ=0)=
| ||||||
|
| 2 |
| 9 |
P(ξ=1)=
| ||||||||||||
|
| 23 |
| 45 |
P(ξ=2)=
| ||||||||
|
| 2 |
| 9 |
P(ξ=3)=
| ||||
|
| 2 |
| 45 |
ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 49 |
| 45 |
点评:本题考查概率的估计值,考查离散型随机变量的分布列和数学期望的求法,解题时要注意排列组合知识的合理运用.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 如图,四棱锥P-ABCD的底面ABCD为正方形,PD⊥底面ABCD,PD=AD.
如图,四棱锥P-ABCD的底面ABCD为正方形,PD⊥底面ABCD,PD=AD.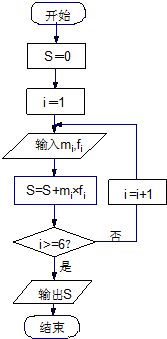 “世界睡眠日”定在每年的3月21日,2009年的世界睡眠日主题是“科学管理睡眠”,以提高公众对健康睡眠的自我管理能力和科学认识.为此某网站于2009年3月13日到3月20日持续一周网上调查公众日平均睡眠的时间(单位:小时),共有2000人参加调查,现将数据整理分组后如题中表格所示.
“世界睡眠日”定在每年的3月21日,2009年的世界睡眠日主题是“科学管理睡眠”,以提高公众对健康睡眠的自我管理能力和科学认识.为此某网站于2009年3月13日到3月20日持续一周网上调查公众日平均睡眠的时间(单位:小时),共有2000人参加调查,现将数据整理分组后如题中表格所示. 如图所示,△ABC内接于⊙O,AB=AC,直线XY切⊙O于点C,BD∥XY,AC、BD相交于E.
如图所示,△ABC内接于⊙O,AB=AC,直线XY切⊙O于点C,BD∥XY,AC、BD相交于E. 如图,在直三棱柱ABC-A1B1C1中,AC=BC=BB1=2.AB=2
如图,在直三棱柱ABC-A1B1C1中,AC=BC=BB1=2.AB=2