题目内容
已知函数m(x)=log4(4x+1),n(x)=kx(k∈R).
(1)若F(x)为R上的奇函数,且当x>0时,F(x)=m(x),求当x<0时F(x)的表达式;
(2)已知f(x)=m(x)+n(x)为偶函数.
①求k的值;
②设g(x)=log4(a•2x-
a),若函数f(x)与g(x)的图象有且只有一个公共点,求实数a的取值范围.
(1)若F(x)为R上的奇函数,且当x>0时,F(x)=m(x),求当x<0时F(x)的表达式;
(2)已知f(x)=m(x)+n(x)为偶函数.
①求k的值;
②设g(x)=log4(a•2x-
| 4 |
| 3 |
考点:对数函数图象与性质的综合应用,函数奇偶性的性质
专题:综合题,函数的性质及应用
分析:(1)运用奇偶性求解运算,得解析式.
(2)f(x)=m(x)+n(x)为偶函数.运用定义恒成立求解.函数f(x)与g(x)的图象有且只有一个公共点,方程log4 (4x+1)-
x=log4(a•2x-
a)只有一个解,即log
=log
,方程等价于
.设 2x=t>0,则(a-1)t2-
at-1=0有一正根,构造函数,分类讨论求解的出答案.
(2)f(x)=m(x)+n(x)为偶函数.运用定义恒成立求解.函数f(x)与g(x)的图象有且只有一个公共点,方程log4 (4x+1)-
| 1 |
| 2 |
| 4 |
| 3 |
4 |
(a•2x-
4 |
|
| 4 |
| 3 |
解答:
解:(1)设x<0,则-x>0,∴F(-x)=m(-x)=log
,
∵F(x为R上的奇函数,∴F(-x)=-F(x),
∴F(x)=-log
(x<0)
(2)①∵函数f(x)=log
+kx是偶函数,
∴f(-x)=log
-kx=log(
)-kx
=log
-(k+1)x=log4(4x+1)+kx=f(-x)(恒成立).
∴-(k+1)=-k,则k=-
.
②∵函数f(x)与g(x)的图象有且只有一个公共点,
∴方程f(x)=g(x)只有一个解
即方程log4 (4x+1)-
x=log(a•2x-
a)只有一个解,
∴log
=log
,
方程等价于
.
设t=2x,t>0,则(a-1)t2-
at-1=0有一正根,
(ⅰ)若a-1>0,设h(t)=(a-1)t2-
at-1,
∵h(0)=-1<0,∴恰好有一正根,∴a>1满足题意;
(ⅱ)若a-1=0,则方程根为t=-
<0,不满足题意;
(ⅲ)若a-1<0,即a<1时,由△=(-
a)2+4(a-1)=0,得a=-3或a=
,
当a=-3时,方程有根t=
满足题意,
当a=
时,方程有根t=-2(舍去).
综上所述,实数a的取值范围是{a|a>1或a=-3}
4-x+1 4 |
∵F(x为R上的奇函数,∴F(-x)=-F(x),
∴F(x)=-log
(4-x+1) 4 |
(2)①∵函数f(x)=log
(4x+1) 4 |
∴f(-x)=log
(4-x+1) 4 |
| 1+4x |
| 4x |
=log
(4x+1) 4 |
∴-(k+1)=-k,则k=-
| 1 |
| 2 |
②∵函数f(x)与g(x)的图象有且只有一个公共点,
∴方程f(x)=g(x)只有一个解
即方程log4 (4x+1)-
| 1 |
| 2 |
| 4 |
| 3 |
∴log
4 |
(a•2x-
4 |
方程等价于
|
设t=2x,t>0,则(a-1)t2-
| 4 |
| 3 |
(ⅰ)若a-1>0,设h(t)=(a-1)t2-
| 4 |
| 3 |
∵h(0)=-1<0,∴恰好有一正根,∴a>1满足题意;
(ⅱ)若a-1=0,则方程根为t=-
| 3 |
| 4 |
(ⅲ)若a-1<0,即a<1时,由△=(-
| 4 |
| 3 |
| 3 |
| 4 |
当a=-3时,方程有根t=
| 1 |
| 2 |
当a=
| 3 |
| 4 |
综上所述,实数a的取值范围是{a|a>1或a=-3}
点评:本题综合考查了对数函数的性质,奇偶性的性质,运算化简比较麻烦,需要的能力较多.

练习册系列答案
相关题目
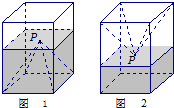 如图1,一个正四棱柱形(底面是正方形)的密闭容器底部镶嵌了同底的正四棱锥形实心装饰块(内部不渗水),容器内盛有a升水时,水面恰好经过正四棱锥的顶点P.如果将容器倒置,水面也恰好过点P(图2).有下列四个命题:
如图1,一个正四棱柱形(底面是正方形)的密闭容器底部镶嵌了同底的正四棱锥形实心装饰块(内部不渗水),容器内盛有a升水时,水面恰好经过正四棱锥的顶点P.如果将容器倒置,水面也恰好过点P(图2).有下列四个命题: